当前位置：首页 > 行业动态 > 正文

coordinate system相关疑问，坐标系统具体包含哪些要素？

Coordinate system refers to a method for uniquely determining the position of points in space using numbers.

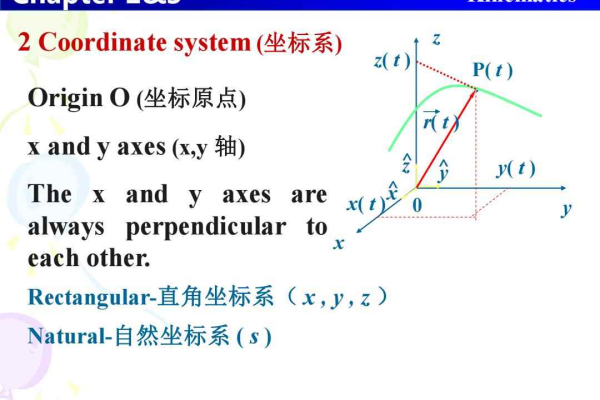
在数学和物理学中，坐标系统是一种用于确定空间中点的位置的系统，它通过一组数值（坐标）来描述点相对于参考系的位置，坐标系统有多种类型，包括笛卡尔坐标系、极坐标系、球坐标系等，下面将详细介绍这些坐标系统及其特点。

坐标系统	特点	应用
笛卡尔坐标系	由两个或三个相互垂直的轴组成，分别用x、y、z表示，每个点的位置由一个有序数对（二维）或有序三元组（三维）表示。	广泛应用于几何学、代数学、物理学等领域。
极坐标系	由一个原点和一个极轴组成，每个点的位置由一个半径r和一个角度θ表示，与笛卡尔坐标系的转换关系为：x = r * cos(θ)，y = r * sin(θ)。	常用于描述圆形、螺旋形等具有对称性的图形，以及在电磁学、流体力学等领域中的应用。
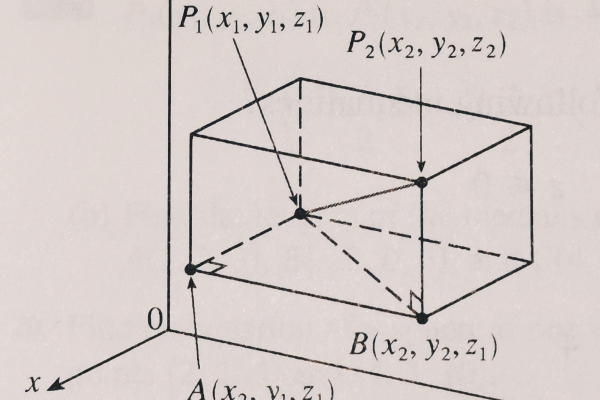
球坐标系	由一个原点、一个极轴和一个赤道平面组成，每个点的位置由一个半径r、一个极角θ和一个方位角φ表示，与笛卡尔坐标系的转换关系为：x = r * sin(θ) * cos(φ)，y = r * sin(θ) * sin(φ)，z = r * cos(θ)。	常用于描述球形、椭球形等具有球对称性的物体，以及在天文学、地球物理学等领域中的应用。