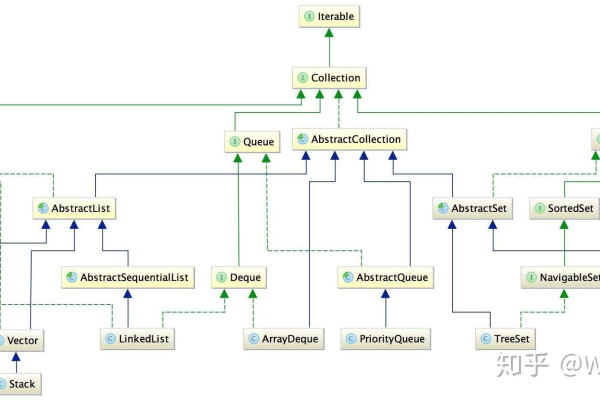
存储结构具体是什么

存储结构是数据元素及其逻辑关系在计算机中的表示，包括顺序、链式、索引和哈希（或散列）存储结构等。

存储结构在计算机科学中是一个核心概念，它指的是数据在计算机内的组织、管理和存储方式，不同的存储结构适用于不同的应用场景，选择合适的存储结构可以有效提高数据处理的效率和性能，下面将详细探讨几种常见的存储结构及其特点。

数组（Array）

定义：数组是一种线性存储结构，它将相同类型的元素按顺序存储在连续的内存空间中，每个元素通过一个索引来访问，索引通常从0开始。

特点：

随机访问：可以通过索引快速访问任意元素，时间复杂度为O(1)。

固定大小：数组的大小在创建时确定，无法动态调整。

内存连续性：数组元素在内存中是连续存储的，有利于缓存优化。

示例：

arr = [1, 2, 3, 4, 5]  # 创建一个包含5个整数的数组
print(arr[2])  # 输出: 3

链表（Linked List）

定义：链表是一种非线性存储结构，由一系列节点组成，每个节点包含数据部分和指向下一个节点的指针（或引用）。

特点：

动态大小：链表可以根据需要动态增加或删除节点。

非连续存储：节点在内存中可以是不连续的，通过指针连接。

插入和删除效率高：在已知位置插入或删除节点的时间复杂度为O(1)。

类型：

单链表：每个节点只包含一个指向下一个节点的指针。

双链表：每个节点包含两个指针，分别指向前一个和后一个节点。

循环链表：最后一个节点指向头节点，形成环状结构。

示例（Python中的单链表实现）：

class Node:
    def __init__(self, data):
        self.data = data
        self.next = None
class LinkedList:
    def __init__(self):
        self.head = None
    def append(self, data):
        new_node = Node(data)
        if not self.head:
            self.head = new_node
            return
        last_node = self.head
        while last_node.next:
            last_node = last_node.next
        last_node.next = new_node
使用链表
linked_list = LinkedList()
linked_list.append(1)
linked_list.append(2)
linked_list.append(3)

栈（Stack）

定义：栈是一种后进先出（LIFO, Last In First Out）的线性存储结构，只允许在一端进行插入和删除操作。

特点：

后进先出：最后进入的元素最先被弹出。

操作受限：主要操作包括push（入栈）和pop（出栈）。

应用场景：函数调用栈、表达式求值、浏览器后退按钮等。

示例（Python中的栈实现）：

stack = []
stack.append(1)  # 入栈
stack.append(2)
print(stack.pop())  # 出栈并输出: 2

队列（Queue）

定义：队列是一种先进先出（FIFO, First In First Out）的线性存储结构，只允许在一端插入元素，在另一端删除元素。

特点：

先进先出：最先进入的元素最先被移出。

操作受限：主要操作包括enqueue（入队）和dequeue（出队）。

应用场景：任务调度、广度优先搜索（BFS）、缓冲区等。

类型：

循环队列：使用数组实现，通过模运算实现循环。

链队列：使用链表实现，便于动态扩展。

示例（Python中的队列实现）：

from collections import deque
queue = deque()
queue.append(1)  # 入队
queue.append(2)
print(queue.popleft())  # 出队并输出: 1

树（Tree）

定义：树是一种层次型存储结构，由一个根节点和若干个子树组成，每个子树也是一个树结构。

特点：

层次结构：具有明确的层次关系，适合表示具有层次性的数据。

节点度：每个节点可以有零个或多个子节点。

遍历方式：包括前序遍历、中序遍历、后序遍历和层序遍历。

类型：

二叉树：每个节点最多有两个子节点。

平衡二叉树：如AVL树、红黑树，保持树的高度尽量平衡。

B树/B+树：用于数据库和文件系统索引，支持高效的范围查询和顺序访问。

示例（二叉树的简单实现）：

class TreeNode:
    def __init__(self, value):
        self.value = value
        self.left = None
        self.right = None
构建一个简单的二叉树
root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.left = TreeNode(4)
root.left.right = TreeNode(5)

图（Graph）

定义：图是由节点（顶点）和边组成的非线性存储结构，用于表示对象之间的复杂关系。

特点：

灵活性高：可以表示多种关系，如社交网络、网络路由等。

遍历算法：深度优先搜索（DFS）、广度优先搜索（BFS）、最短路径算法等。

存储方式：邻接矩阵、邻接表等。

类型：

无向图：边没有方向。

有向图：边有方向。

带权图：边上带有权重，表示距离、成本等。

示例（使用邻接表表示图）：

graph = {
    'A': ['B', 'C'],
    'B': ['A', 'D', 'E'],
    'C': ['A', 'F'],
    'D': ['B'],
    'E': ['B', 'F'],
    'F': ['C', 'E']
}

哈希表（Hash Table）

定义：哈希表是一种基于哈希函数的数据结构，通过哈希函数将键映射到哈希表中的槽位，以实现快速的查找、插入和删除操作。

特点：

快速访问：平均时间复杂度为O(1)，但最坏情况下可能退化为O(n)。

处理冲突：通过链地址法、开放地址法等方式解决哈希冲突。

应用广泛：用于实现字典、集合等高级数据结构，以及缓存机制。

示例（Python中的字典作为哈希表的一种实现）：

hash_table = {}
hash_table['key1'] = 'value1'
hash_table['key2'] = 'value2'
print(hash_table['key1'])  # 输出: value1

堆（Heap）

定义：堆是一种特殊的完全二叉树，分为最大堆和最小堆，用于实现优先级队列。

特点：

完全二叉树：除了最后一层外，其他层都是满的，且最后一层的节点都靠左排列。

堆性质：最大堆中父节点的值大于等于子节点的值；最小堆中父节点的值小于等于子节点的值。

高效操作：插入和删除操作的时间复杂度为O(log n)。

示例（Python中的堆实现）：

import heapq
heap = []
heapq.heappush(heap, 1)  # 插入元素
heapq.heappush(heap, 3)
print(heapq.heappop(heap))  # 弹出并返回最小元素: 1

9. 散列表（Hash Table）与布隆过滤器（Bloom Filter）

散列表（Hash Table）：前面已提及，是一种基于哈希函数的数据结构，用于快速查找、插入和删除操作，通过哈希函数将键映射到散列表中的槽位，以实现高效的数据操作，散列表的平均时间复杂度为O(1)，但最坏情况下可能退化为O(n)，为了处理哈希冲突，散列表采用了链地址法、开放地址法等技术，散列表在实际应用中非常广泛，如数据库索引、缓存机制等。

布隆过滤器（Bloom Filter）：布隆过滤器是一种空间效率极高的概率型数据结构，用于测试一个元素是否在一个集合中，它使用多个哈希函数将元素映射到一个位数组中，通过检查这些位是否都被置位来判断元素是否存在，布隆过滤器的主要优点是空间占用小，但有一定的误判率（即可能会错误地认为某个不在集合中的元素存在），布隆过滤器常用于网络爬虫的URL判重、垃圾邮件过滤等领域。

FAQs

Q1: 为什么数组的大小是固定的？

A1: 数组在创建时需要分配一块连续的内存空间，因此其大小是固定的，一旦数组满了，需要创建一个新的更大的数组并复制旧数组的元素，这称为“扩容”，但频繁的扩容会影响性能，所以通常在初始化时就尽量估计好所需的大小。

Q2: 链表和数组相比有什么优势？

A2: 链表的主要优势在于其动态性，可以在运行时根据需要动态地添加或删除节点，而不需要像数组那样预先分配固定大小的内存，链表在插入和删除操作上通常比数组更高效，因为不需要移动其他元素，链表的缺点是访问速度较慢，因为需要从头开始遍历链表来找到特定的节点，而数组则可以通过索引直接访问元素，速度更快。

Q3: 栈和队列有什么区别？

A3: 栈是后进先出（LIFO）的数据结构，意味着最后进入栈的元素会最先被弹出，而队列是先进先出（FIFO）的数据结构，意味着最先进入队列的元素会最先被移出，这两种数据结构在操作顺序上有所不同，栈主要用于实现递归、表达式求值等功能，而队列则常用于任务调度、消息传递等场景。

Q4: 二叉树和平衡二叉树有什么不同？

A4: 二叉树是每个节点最多有两个子节点的树结构，而平衡二叉树（如AVL树、红黑树）是在二叉树的基础上增加了平衡条件，即任何节点的两个子树的高度差不能超过1，平衡二叉树通过旋转等操作来保持树的平衡，从而保证在最坏情况下查找、插入和删除操作的时间复杂度都是O(log n)，而普通的二叉树可能会退化成链表，导致操作效率低下。