当前位置：首页 > 行业动态 > 正文

光照不均匀图像的频域增强方法

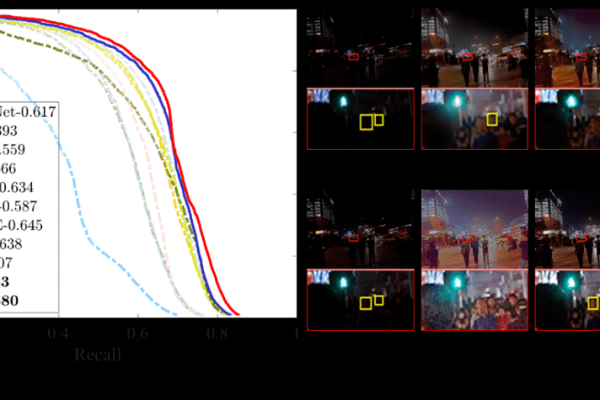
针对光照不均匀图像，频域增强方法通过傅里叶变换将图像转换至频域，设计同态滤波器抑制低频光照背景，增强高频细节信息，结合对数变换平衡亮度，最后逆变换重构图像，有效改善光照不均问题

光照不均匀图像的频域增强方法

频域增强的基本原理

光照不均匀的图像通常表现为低频背景亮度变化显著，而高频细节（如边缘、纹理）被掩盖，频域增强的核心是通过傅里叶变换将图像从空间域转换到频率域，分离低频和高频成分，并对不同频率分量进行针对性处理。

光照不均匀图像的频域增强方法

  • 低频成分：对应光照不均匀的背景，需抑制或平滑。
  • 高频成分：对应图像细节，需保留或增强。

关键步骤与实现方法

步骤 方法描述 技术要点
预处理 对数变换（Logarithmic Transformation） 将乘性光照分量转化为加性分量，公式：s = log(1 + r)，其中r为输入图像灰度值。
傅里叶变换 转换到频域 使用快速傅里叶变换（FFT）获取频谱，频谱中心为低频，外围为高频。
滤波器设计 高通滤波器或同态滤波器 理想高通滤波器：直接抑制低频，保留高频。
同态滤波器：结合光照和反射模型，对低频和高频分别设计衰减函数（如高斯滤波器）。
逆傅里叶变换 转换回空间域 通过逆FFT还原图像，得到增强后的图像。
后处理 伽马校正（Gamma Correction） 调整亮度感知，公式：s = s^(1/γ)，通常γ < 1以提亮暗区。

典型滤波器对比

滤波器类型 低频抑制强度 高频保留效果 适用场景
理想高通滤波器 强（直接截断） 弱（可能丢失细节） 光照差异极大但细节少的图像
高斯高通滤波器 中等（平滑过渡） 较好（保留边缘） 一般光照不均图像
同态滤波器 可调节（灵活控制） 最佳（平衡光照与细节） 复杂场景（如医学影像、文档扫描）

参数调整策略

  • 对数变换参数：s = log(1 + r)中的+1避免r=0时log无定义。
  • 滤波器截止频率：低频截止频率越高，光照抑制越强，但可能损失细节。
  • 伽马值（γ）：越小，暗区提亮越明显，但可能降低整体对比度。

优缺点分析

优点 缺点
直接处理频率成分，物理意义明确 计算复杂度高（需FFT和逆FFT）
可灵活调整低频/高频权重 参数选择敏感，易出现过度增强或噪声
适用于全局光照不均问题 对局部强光（如亮点）处理效果有限

相关问题与解答

问题1：为什么需要对数变换预处理？

解答：
光照不均的图像可建模为I(x,y) = L(x,y) R(x,y)，其中L为低频光照分量，R为高频反射分量，直接频域滤波难以分离两者，因为乘法关系导致频率混叠，对数变换s = log(1 + I)将乘法转为加法（log(LR) = log(L) + log(R)），使光照和反射分量在频域中独立，便于分别处理。

光照不均匀图像的频域增强方法

问题2：同态滤波相比普通高通滤波的优势是什么？

解答：
普通高通滤波器直接抑制所有低频成分，可能导致光照区域过暗或细节丢失，同态滤波通过设计非线性滤波器（如高斯函数），对低频光照分量和高频反射分量采用不同衰减策略：

光照不均匀图像的频域增强方法

  • 低频（光照）：适度衰减，避免完全抑制导致图像发暗。
  • 高频（细节）：保留或增强，提升对比度。
    这种灵活性使其在复杂光照场景中表现更

相关文章