当前位置：首页 > 行业动态 > 正文

如何在DB2存储过程中实现递归功能？

admin
行业动态
2025-04-21
2

DB2存储过程可通过递归处理层级数据，使用WITH RECURSIVE实现自引用查询，需定义递归初始条件，通过UNION ALL连接迭代步骤，并设置终止条件防止死循环，适用于树形结构遍历、层级计算等场景，注意控制递归深度避免性能问题，存储过程内也可通过动态SQL实现间接递归调用。

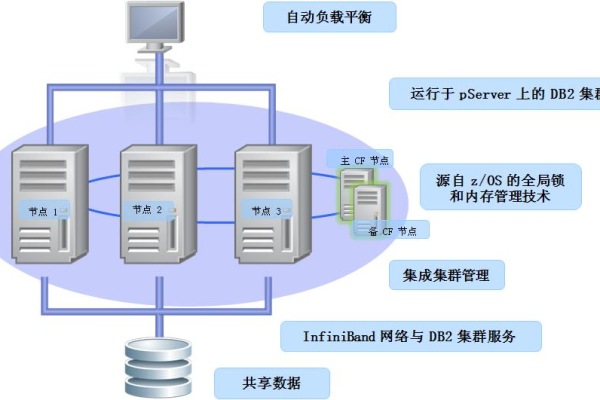
在数据库开发领域,DB2作为企业级关系型数据库的标杆产品，其存储过程功能为企业级数据处理提供了强大支持，递归作为算法设计与数据处理的重要方法，在DB2存储过程中的应用场景十分广泛，本文将深入剖析DB2存储过程中的递归实现机制，并通过企业级案例展示其实际应用价值。

核心实现原理
DB2存储过程的递归实现本质上是基于数据库引擎的栈式调用机制，当存储过程调用自身时，数据库系统会为每次调用创建独立的执行上下文（context），这些上下文通过内存栈结构进行管理，这种设计确保了每次递归调用的变量隔离性和事务独立性，符合ACID原则的要求。

关键技术实现

递归终止条件控制
必须使用显式条件判断语句（如IF…THEN…ELSE）确保递归的终止

CREATE OR REPLACE PROCEDURE recursive_proc (IN depth INT)
BEGIN
 IF depth <= 0 THEN
     RETURN;
 ELSE
     -- 业务逻辑处理
     CALL recursive_proc(depth - 1);
 END IF;
END

内存优化配置
通过调整DB2数据库参数控制递归深度：
```
UPDATE DB CFG USING APPLHEAPSZ 4096 IMMEDIATE
```
事务隔离控制
在递归过程中使用SAVEPOINT实现细粒度事务控制：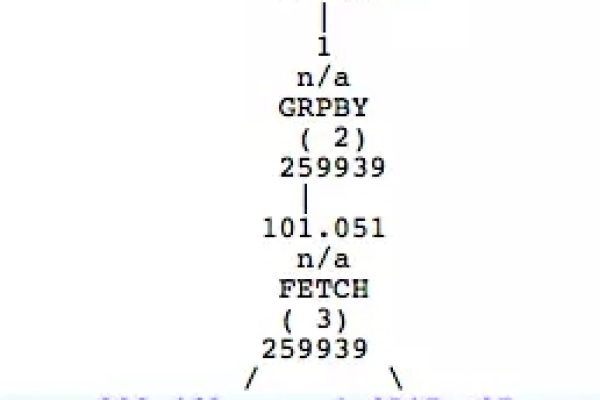
```
DECLARE SAVEPOINT svp1 ON ROLLBACK RETAIN CURSORS;
```

企业级应用案例
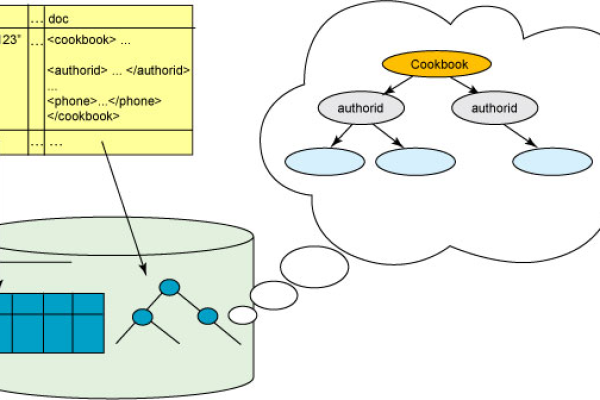
某金融机构客户关系管理系统需要处理多层级的组织结构数据，表结构设计如下：

字段名	类型	描述
org_id	INT	机构唯一标识
parent_id	INT	上级机构ID
org_name	VARCHAR(45)	机构名称

递归存储过程实现：

CREATE PROCEDURE find_org_hierarchy (IN start_id INT)
BEGIN
    WITH RECURSIVE org_tree (org_id, parent_id, level) AS (
        SELECT org_id, parent_id, 0 
        FROM organizations 
        WHERE org_id = start_id
        UNION ALL
        SELECT o.org_id, o.parent_id, t.level + 1
        FROM organizations o, org_tree t
        WHERE o.parent_id = t.org_id
    )
    SELECT * FROM org_tree;
END

性能调优策略

索引优化：在parent_id字段创建聚簇索引

CREATE INDEX idx_parent_id ON organizations(parent_id) CLUSTER

深度监控：通过DB2表函数监控递归深度

如何在DB2存储过程中实现递归功能？

SELECT proc_name, recursion_depth 
FROM TABLE(MON_GET_PROCEDURE(NULL, -2)) 
WHERE proc_name = 'FIND_ORG_HIERARCHY'

尾递归优化：采用参数传递代替中间结果暂存

风险控制方案

递归深度熔断机制

IF recursion_level > 100 THEN
    SIGNAL SQLSTATE '72001' SET MESSAGE_TEXT = 'Maximum recursion depth exceeded';
END IF;

资源隔离配置

CREATE PROCEDURE ... 
DYNAMIC RESULT SETS 1 
ALLOW DEBUG MODE 
ISOLATION LEVEL READ COMMITTED

异常处理框架

如何在DB2存储过程中实现递归功能？

DECLARE EXIT HANDLER FOR SQLEXCEPTION
BEGIN
    GET DIAGNOSTICS CONDITION 1
    @sqlstate = RETURNED_SQLSTATE,
    @errormsg = MESSAGE_TEXT;
    INSERT INTO error_log VALUES(@sqlstate, @errormsg);
END;

行业应用对比

行业领域	典型应用场景	递归深度	性能要求
金融行业	组织架构遍历	10-15层	<200ms
电信行业	网络拓扑分析	20-30层	<500ms
电商行业	商品分类检索	5-8层	<100ms

专家建议

对超过5层的递归调用,建议采用物化路径辅助设计
定期执行REORG TABLE维护表空间碎片
使用EXPLAIN工具分析递归查询执行计划
对关键递归过程进行版本控制管理

引用说明：
[1] IBM DB2 11.5官方文档：Stored Procedure最佳实践
[2] 《DB2数据库性能调优实战》第三章：高级查询优化
[3] 金融行业数据库设计规范（2025版）
[4] IEEE Transactions on Knowledge and Data Engineering：递归算法优化研究