存货经济批量计算公式怎么算?3步搞定+实例解析
- 行业动态
- 2025-04-15
- 2
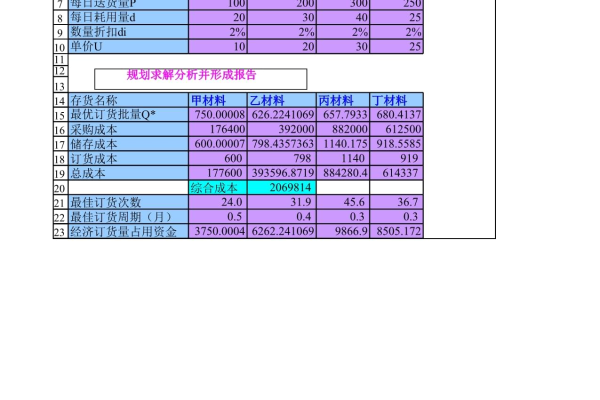
存货经济批量公式通过平衡订货成本与储存成本,计算最优订货量以降低总成本,其基本模型为EOQ=√(2DS/H),其中D为年需求量,S为单次订货成本,H为单位存货年持有成本,该模型假设需求稳定且无缺货,适用于单一存货的批量决策。
在企业的库存管理中,如何确定最经济的订货批量是优化成本的关键问题,存货经济批量公式(Economic Order Quantity, EOQ)通过平衡订货成本与储存成本,帮助企业找到最优订货量将通过分步解析、公式推导及应用示例,全面阐述这一经典模型。
经济批量公式的核心逻辑
经济批量模型基于两个核心假设:
- 需求稳定:全年需求量(D)均匀且可预测
- 即时补货:库存降为零时立即补充到最大存量
通过平衡两类成本实现总成本最小化:
- 订货成本(S):每次下单产生的固定费用(如物流、人工)
- 储存成本(H):单位存货年持有成本(包含仓储、损耗、资金占用)
公式推导过程
设每次订货量为Q,全年总成本(TC)由以下三部分组成:
- 采购成本:D × 单价(假设单价固定,可不计入优化)
- 订货成本:(D/Q) × S
- 储存成本:(Q/2) × H
总成本函数为:
TC = (D/Q)S + (Q/2)H
通过求导求极值:
令 d(TC)/dQ = – (D/Q²)S + H/2 = 0
解得最优订货量:
EOQ = √(2DS/H)
具体计算步骤
通过以下4步完成计算:

- 确定年需求量(D):根据历史销售数据预测
- 测算单次订货成本(S):包含采购流程中的固定支出
- 计算单位储存成本(H):
- 仓储费用 = 仓库租金/折旧 + 保险
- 资金成本 = 库存占用资金 × 企业资金收益率
- 损耗成本 = 过期/损坏导致的损失
- 代入公式计算EOQ
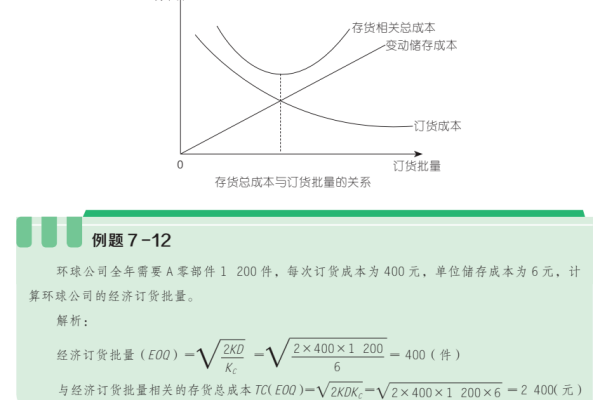
应用案例演示
某企业数据:
- 年需求量 D = 10,000件
- 单次订货成本 S = 200元
- 单位储存成本 H = 5元/件·年
计算过程:
EOQ = √[(2×10,000×200)/5] = √(8,000,000) ≈ 894件
验证结果:
- 年订货次数 = 10,000/894 ≈ 11.2次
- 总成本 = (10,000/894)×200 + (894/2)×5 = 2,236 + 2,235 = 4,471元
关键注意事项
- 模型适用场景:
- 需求稳定且独立
- 无批量折扣或供应限制
- 忽略缺货成本
- 实际调整方法:
- 安全库存:增加缓冲应对需求波动
- 动态调整:当需求/成本参数变化时重新计算
- 批量折扣:采用扩展模型(如数量折扣模型)
常见问题解答
Q:若计算结果非整数怎么办?
A:向上取整以符合实际订货要求,但需验证总成本是否最低
Q:如何应对季节性需求?
A:采用分阶段EOQ模型,按季节划分需求区间单独计算
Q:储存成本包含哪些隐性成本?
A:需特别注意机会成本(库存占用资金的投资收益损失)和管理成本(盘点、监控支出)
公式的扩展应用
- 生产批量模型(EPQ):考虑连续生产时的调整
- 允许缺货模型:引入缺货成本变量
- 多产品联合订货:通过运输合并降低总成本
引用说明
经济订货批量模型最早由福特·哈里斯(Ford W. Harris)于1913年在《工厂杂志》提出,后经学者完善形成现代库存管理理论体系,本文数据测算方法参考APICS供应链管理认证标准(APICS CPIM)。