马里服务器租用收费价格都与哪些方面有关联
- 行业动态
- 2024-04-10
- 4
马里服务器租用收费价格通常与服务器的硬件配置、带宽、IP数量、机房等级及服务支持水平等因素紧密相关。
马里服务器租用收费价格通常与以下几个因素有关:
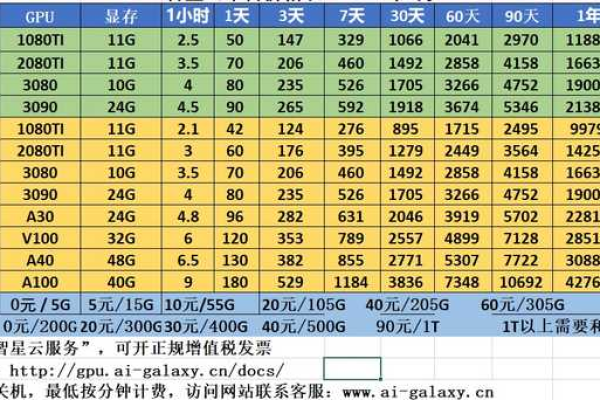
1、服务器配置
2、带宽和流量
3、IP地址数量
4、机房设施
5、技术支持和服务
6、合同期限
下面是这些因素的详细说明:
1. 服务器配置
服务器的配置是影响价格的主要因素之一,包括CPU型号、核心数、内存大小、硬盘类型和容量等,更高的配置通常意味着更高的价格。
| 配置项 | 低配 | 中配 | 高配 |
| CPU | 低端型号,少量核心 | 中端型号,适中核心 | 高端型号,多核心 |
| 内存 | 小容量(如8GB) | 中等容量(如16GB) | 大容量(如32GB以上) |
| 硬盘 | 小容量SSD或HDD | 中等容量SSD或HDD | 大容量SSD或NVMe |
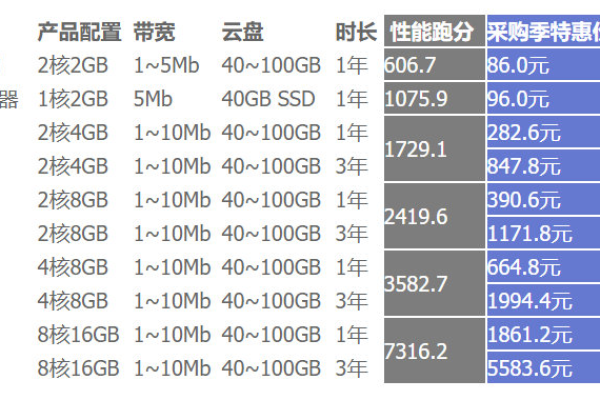
2. 带宽和流量
带宽和流量也是决定服务器租用价格的重要因素,更大的带宽和流量意味着更高的数据传输能力,但也会导致成本增加。
| 类型 | 共享带宽 | 独享带宽 |
| 价格 | 较低 | 较高 |
3. IP地址数量
IP地址的数量也会影响价格,通常,一个IP地址是免费的,但额外的IP地址可能会收取额外费用。
| IP数量 | 1个 | 多个 |
| 价格 | 较低 | 较高 |
4. 机房设施
机房的设施和条件也会影响价格,优质的机房通常提供更好的网络连接、电力供应和冷却系统,但价格相对较高。
| 机房等级 | 普通 | 优质 |
| 价格 | 较低 | 较高 |
5. 技术支持和服务
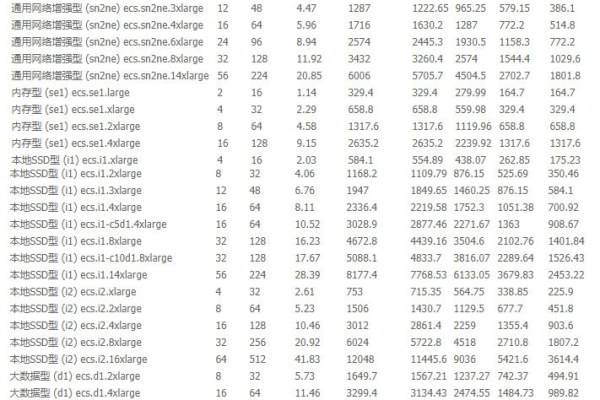
不同的服务提供商可能会提供不同级别的技术支持和服务,更好的技术支持和服务通常意味着更高的价格。
| 服务水平 | 基本 | 高级 |
| 价格 | 较低 | 较高 |
6. 合同期限
合同期限也是影响价格的因素之一,长期合同可能会获得一定的折扣,而短期合同可能价格较高。
| 期限 | 短期 | 长期 |
| 价格 | 较高 | 较低 |
马里服务器租用收费价格与服务器配置、带宽和流量、IP地址数量、机房设施、技术支持和服务以及合同期限等因素密切相关,在选择服务器租用时,需要根据实际需求和预算来综合考虑这些因素。
















