bp神经网络程序的报告

BP神经网络（Backpropagation Neural Network）是一种基于误差反向传播算法训练的多层前馈神经网络，广泛应用于模式识别、数据预测、分类任务等领域，本报告将深入解析BP神经网络的原理、程序实现的关键步骤，并探讨其实际应用场景,帮助读者全面理解该算法的核心价值。

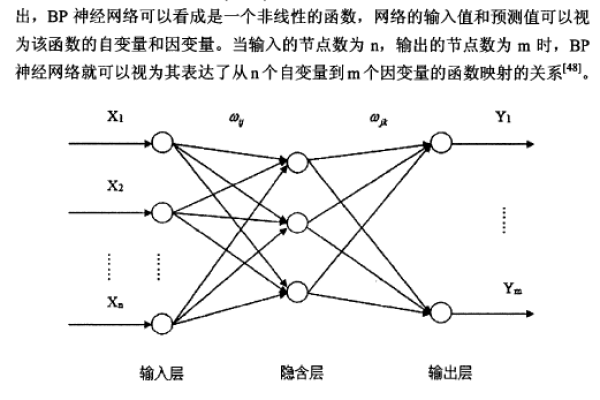
BP神经网络的核心原理

BP神经网络通过“前向传播”和“反向传播”两个阶段完成学习过程：

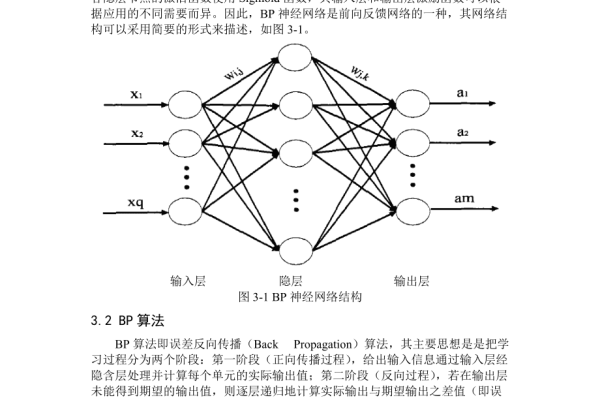
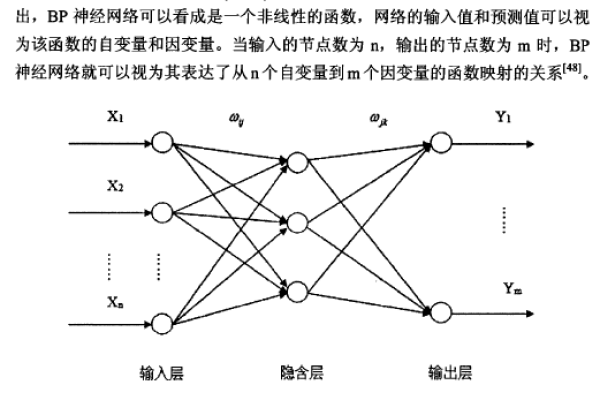
1. 前向传播：输入数据逐层传递至隐藏层和输出层，计算预测结果。
2. 反向传播：根据预测结果与真实值的误差，利用梯度下降法调整网络权重，通过链式法则逐层更新参数。

关键公式：

• 输出误差计算：( E = frac{1}{2}sum (y{text{真实}} – y{text{预测}})^2 )
• 权重更新：( Delta w{ij} = -eta frac{partial E}{partial w{ij}} )（( eta )为学习率）

该算法通过迭代优化权重,使网络输出逐步逼近真实值。

程序实现的关键步骤

以Python语言为例，结合NumPy库实现BP神经网络的核心流程如下：

数据准备与预处理

• 标准化数据：对输入特征进行归一化处理，例如使用Z-score标准化。
• 标签编码：分类任务需将标签转为独热编码（One-Hot Encoding）。

网络结构设计

• 输入层节点数：与特征维度一致（如28×28图像对应784个节点）。
• 隐藏层配置：通常1-2层，每层节点数需通过实验调整（如128或256）。
• 输出层节点数：分类任务中等于类别数，回归任务中为1。

参数初始化

• 权重矩阵：采用Xavier初始化，避免梯度消失或爆炸。
• 偏置项：初始值常设为0或微小随机数。

import numpy as np
def initialize_parameters(layer_dims):
    parameters = {}
    for l in range(1, len(layer_dims)):
        parameters['W' + str(l)] = np.random.randn(layer_dims[l], layer_dims[l-1]) * 0.01
        parameters['b' + str(l)] = np.zeros((layer_dims[l], 1))
    return parameters

激活函数选择

• 隐藏层：常用ReLU（加速收敛）或Sigmoid函数。
• 输出层：分类任务用Softmax，回归任务用线性函数。

训练与优化

• 批量训练：每次迭代使用小批量数据（Mini-Batch）计算梯度。
• 学习率衰减：随着训练轮次增加，逐步降低学习率以提高收敛稳定性。

实际应用场景与案例分析

图像识别

• 案例：手写数字识别（如MNIST数据集）。
• 效果：通过3层网络（784-128-10）可实现98%以上的准确率。

金融预测

• 案例：股票价格趋势预测。
• 策略：输入历史价格、交易量等特征，输出未来涨跌概率。

自然语言处理

• 案例：文本情感分析。
• 方法：将词向量作为输入，输出积极/消极情感分类。

优势与挑战

优势

• 非线性拟合能力强，适合复杂数据模式。
• 算法成熟，开源框架支持完善（如TensorFlow、PyTorch）。

挑战

• 易陷入局部最优解，需结合Adam优化器等改进策略。
• 超参数（层数、节点数）调优依赖经验。

参考文献

1. Rumelhart, D. E., Hinton, G. E., & Williams, R. J. (1986). Learning representations by back-propagating errors. Nature.
2. Goodfellow, I., Bengio, Y., & Courville, A. (2016). Deep Learning. MIT Press.
3. 周志华. (2016). 机器学习. 清华大学出版社.

通过合理设计网络结构、选择优化策略，BP神经网络能够有效解决多种复杂问题，在实际应用中，建议结合交叉验证、正则化技术进一步提升模型泛化能力。