当前位置：首页 > 行业动态 > 正文

dfa算法js

admin
行业动态
2025-04-05
3

“

javascript，function dfa(states, alphabet, transitionFunction, startState, acceptStates, inputString) {， let currentState = startState;， for (let char of inputString) {， if (!alphabet.includes(char)) {， return false;， }， currentState = transitionFunction[currentState][char];， }， return acceptStates.includes(currentState);，}，

` 这段代码定义了一个dfa`函数，用于根据给定的状态、字母表、转换函数、起始状态和接受状态来判断输入字符串是否被DFA接受。

DFA算法，即确定性有限状态自动机（Deterministic Finite Automaton）算法，是一种在计算机科学中广泛应用的算法，特别是在文本匹配、词法分析和模式识别等领域，以下是对DFA算法的详细解析：

基本原理

DFA是一种数学模型，用于描述有限个状态以及这些状态之间的转移和动作等行为，它主要由一个五元组构成：状态集合、输入字母表、转移函数、初始状态和终止状态集合，对于每一个输入符号，DFA都能根据当前状态和转移函数确定地转移到下一个状态，这种确定性使得DFA在处理输入时非常高效。

特点

1、确定性：对于每个状态和输入符号，DFA都有且仅有一个可能的下一个状态。

2、有限性：状态数量是有限的，输入符号的种类也是有限的。

3、无环性：在DFA的状态转换图中，不存在环路。

应用

DFA算法在多个领域有广泛的应用，包括但不限于：

文本匹配：用于快速查找文本中的特定模式或关键词。

词法分析：编译器使用DFA来识别程序源代码中的标识符、关键字等。

dfa算法js

网络协议分析：用于解析和理解网络协议数据包。

生物信息学：在DNA序列分析中查找特定的基因模式。

实现步骤

以文本匹配为例，实现DFA算法的步骤通常包括：

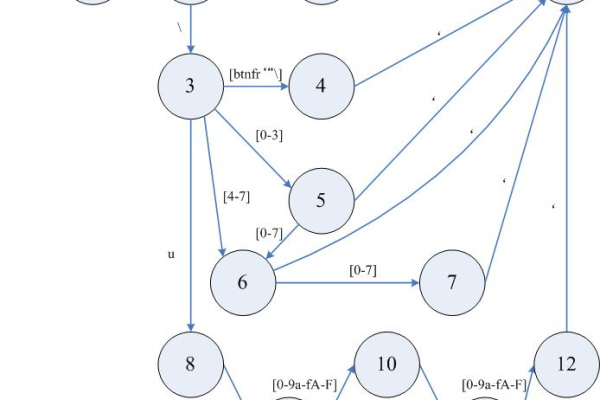
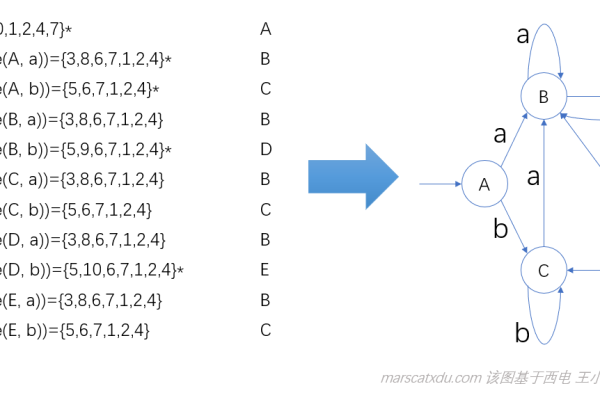
1、构建DFA：根据需要匹配的模式构建DFA的状态转换图。

2、初始化：设置初始状态和输入文本。

3、遍历文本：逐个读取文本中的字符，并根据当前状态和字符更新到下一个状态。

dfa算法js

4、检查终止状态：如果达到终止状态，则表示匹配成功；否则匹配失败。

JavaScript实现示例

以下是一个简单的JavaScript实现示例，用于匹配字符串中的特定模式（如“abc”）：

JavaScript

class DFA {
    constructor(pattern) {
        this.pattern = pattern;
        this.states = {};
        this.buildDFA();
    }
    buildDFA() {
        // 构建DFA的状态转换图
        let state = 0;
        for (let char of this.pattern) {
            if (!this.states[state]) {
                this.states[state] = {};
            }
            state++;
            this.states[state 1][char] = state;
        }
        this.states[state 1][''] = 'accept'; // 终止状态
    }
    match(text) {
        let state = 0;
        for (let char of text) {
            if (this.states[state] && this.states[state][char]) {
                state = this.states[state][char];
            } else {
                return false; // 不匹配
            }
        }
        return this.states[state][''] === 'accept'; // 检查是否到达终止状态
    }
}
// 使用示例
const dfa = new DFA('abc');
console.log(dfa.match('abc')); // 输出: true
console.log(dfa.match('abx')); // 输出: false