Python中素数判断

在Python中，判断一个数是否为素数通常通过检查该数是否能被2到它的平方根之间的任何整数整除。

素数判断是编程中一个经典的问题，它涉及到数学和算法的知识，在Python中，有多种方法可以进行素数的判断，下面将介绍几种常见的方法，并给出相应的代码实现。

方法一：暴力枚举法

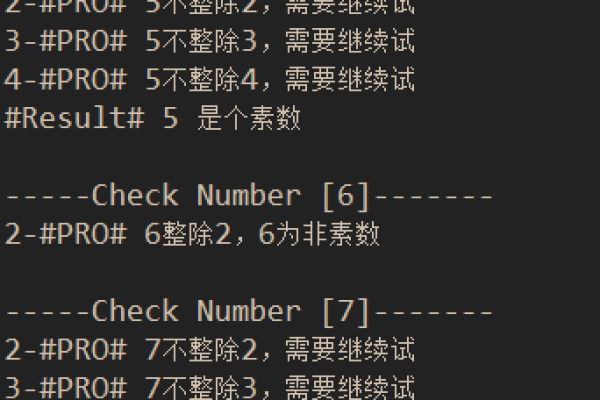
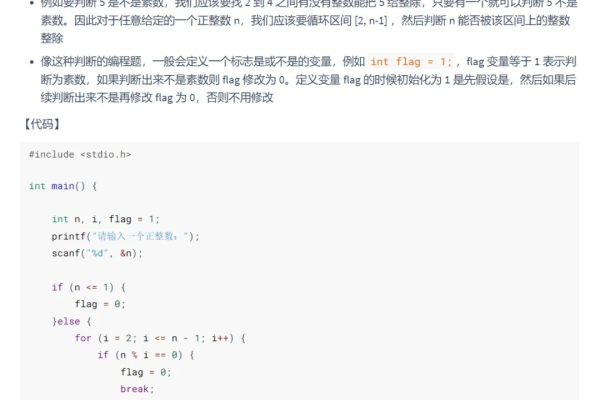
最直观的方法是使用暴力枚举法，即对从2到根号n的所有整数进行遍历，检查n是否能被这些整数整除，如果能找到一个整数使得n能被整除，则n不是素数；否则，n是素数。

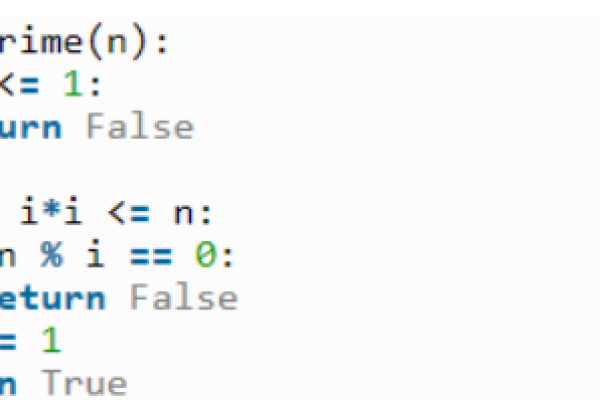
def is_prime(n):
    if n <= 1:
        return False
    for i in range(2, int(n**0.5) + 1):
        if n % i == 0:
            return False
    return True

方法二：埃拉托斯特尼筛法

埃拉托斯特尼筛法是一种高效的素数筛选算法，它的基本思想是从2开始，将所有2的倍数标记为非素数，然后找到下一个未被标记的数，将其所有倍数标记为非素数，依次类推，直到遍历完所有小于等于n的整数。

def sieve_of_eratosthenes(n):
    prime = [True] * (n + 1)
    prime[0] = prime[1] = False
    for p in range(2, int(n**0.5) + 1):
        if prime[p]:
            for i in range(p * p, n + 1, p):
                prime[i] = False
    return [x for x in range(2, n + 1) if prime[x]]

方法三：优化的暴力枚举法

在暴力枚举法的基础上，我们可以进行一些优化，只需要检查到根号n即可，因为大于根号n的因子必定会与小于根号n的因子成对出现，还可以跳过偶数的检查，因为除了2以外的偶数肯定不是素数。

def optimized_is_prime(n):
    if n <= 1:
        return False
    if n == 2:
        return True
    if n % 2 == 0:
        return False
    for i in range(3, int(n**0.5) + 1, 2):
        if n % i == 0:
            return False
    return True

方法四：Miller-Rabin素性测试

Miller-Rabin素性测试是一种概率性的素数判断算法，它基于费马小定理，对于大多数情况下，它的效率非常高，但有一定的误判率，可以通过多次测试来降低误判率。

import random
def miller_rabin_test(n, k=5):   number of tests to run
    if n <= 1 or n == 4:
        return False
    if n <= 3:
        return True
     Find r and d such that n = 2^r * d + 1 for some r >= 1
    d = n 1
    r = 0
    while d % 2 == 0:
        d //= 2
        r += 1
     Witness loop
    for _ in range(k):
        a = random.randint(2, n 2)
        x = pow(a, d, n)
        if x == 1 or x == n 1:
            continue
        for _ in range(r 1):
            x = pow(x, 2, n)
            if x == n 1:
                break
        else:
            return False
    return True

相关问题与解答

问题1：为什么暴力枚举法只需要检查到根号n？

答：如果n是一个合数，那么它必定有一个不大于根号n的因子，只需要检查到根号n即可。

问题2：埃拉托斯特尼筛法的时间复杂度是多少？

答：埃拉托斯特尼筛法的时间复杂度是O(n log log n)。

问题3：优化的暴力枚举法相比原始的暴力枚举法有什么优势？

答：优化的暴力枚举法只需要检查到根号n，并且可以跳过偶数的检查，从而提高了算法的效率。

问题4：Miller-Rabin素性测试的误判率是多少？

答：Miller-Rabin素性测试的误判率取决于测试次数k，当k足够大时，误判率可以忽略不计。