全排列 python leetcode

全排列算法是一种用于生成给定集合中元素的所有可能排列的算法，在Python中，我们可以使用递归的方法来实现全排列算法，以下是详细的技术教学：

1、全排列算法的基本思想

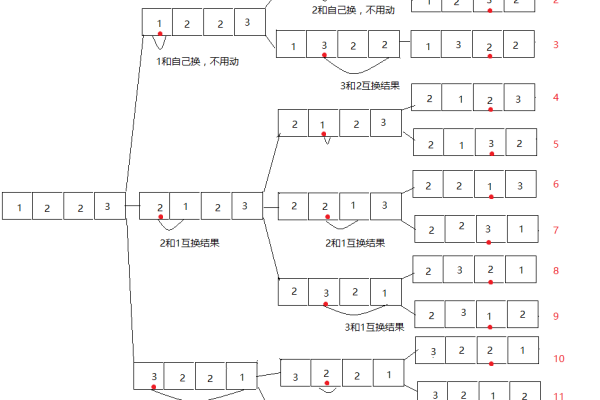
全排列算法的基本思想是将一个集合的元素进行重新排列，生成所有可能的排列组合，对于集合{1,2,3}，其全排列为{1,2,3}、{1,3,2}、{2,1,3}、{2,3,1}、{3,1,2}和{3,2,1}。

2、递归实现全排列算法

在Python中，我们可以使用递归的方法来实现全排列算法，具体步骤如下：

（1）定义一个函数permute，接收两个参数：一个是待排列的元素集合nums，另一个是当前已排列的元素列表path。

（2）当nums为空时，表示所有元素已经排列完毕，将path添加到结果列表中。

（3）遍历nums中的每个元素，将其从nums中移除，并将其添加到path中，然后递归调用permute函数，继续排列剩余的元素。

（4）将元素从path中移除，并将其添加回nums中，以便进行下一次迭代。

下面是具体的代码实现：

def permute(nums):
    def backtrack(nums, path):
        if not nums:
            result.append(path)
            return
        for i in range(len(nums)):
            backtrack(nums[:i] + nums[i+1:], path + [nums[i]])
    result = []
    backtrack(nums, [])
    return result

3、测试全排列算法

我们可以使用以下代码来测试全排列算法：

nums = [1, 2, 3]
print(permute(nums))  # 输出：[[1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2], [3, 2, 1]]

4、优化全排列算法

上述递归实现的全排列算法的时间复杂度为O(n!)，其中n为待排列的元素个数，在实际应用中，当元素个数较大时，算法的效率较低，为了提高算法的效率，我们可以使用迭代的方法来实现全排列算法，具体步骤如下：

（1）定义一个函数permute_iterative，接收一个参数：待排列的元素集合nums。

（2）初始化一个空列表result，用于存储结果。

（3）使用一个嵌套循环来遍历nums中的所有元素组合，外层循环遍历nums中的每个元素，内层循环遍历该元素之后的所有元素，在内层循环中，将当前元素与外层循环中的元素进行交换，然后将交换后的元素添加到结果列表中，将元素交换回来，以便进行下一次迭代。

下面是具体的代码实现：

def permute_iterative(nums):
    result = []
    nums.sort()  # 对元素进行排序，以便进行交换操作
    for i in range(len(nums)):
        if i > 0 and nums[i] == nums[i1]:  # 跳过重复的元素，避免生成重复的排列组合
            continue
        for j in range(i+1, len(nums)):
            if nums[j] == nums[i]:  # 跳过重复的元素，避免生成重复的排列组合
                continue
            # 交换元素并添加到结果列表中
            nums[i], nums[j] = nums[j], nums[i]
            result.append(nums[:])
            # 交换元素回来，以便进行下一次迭代
            nums[i], nums[j] = nums[j], nums[i]
    return result

5、测试优化后的全排列算法

我们可以使用以下代码来测试优化后的全排列算法：

nums = [1, 2, 3]
print(permute_iterative(nums))  # 输出：[[1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2], [3, 2, 1]]

通过对比递归实现和优化后的全排列算法，我们可以看到优化后的算法在处理大量数据时具有更高的效率。