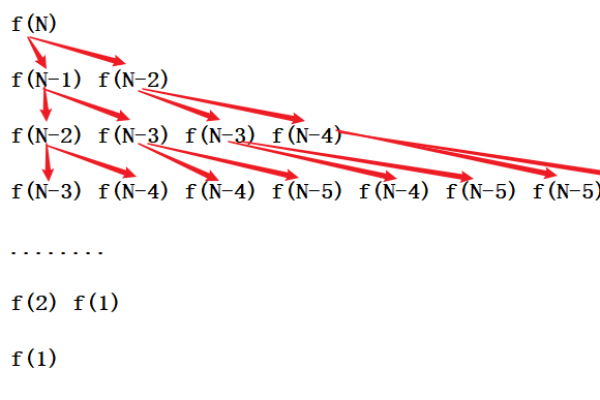递归算法的时间复杂度如何计算？

递归的时间复杂度取决于递归的深度和每次递归的操作量。

在计算机科学中，递归是一种常见的编程技术，它允许函数或过程直接或间接地调用自身，递归算法的时间复杂度分析是理解其性能的关键，本文将探讨递归算法的时间复杂度，并通过表格形式展示不同递归算法的时间复杂度。

递归时间复杂度分析

递归算法的时间复杂度取决于递归的深度和每层递归所做的工作量，我们可以通过以下步骤来分析递归算法的时间复杂度：

1、确定递归关系：找出递归函数调用自身的方式，通常可以用一个递推公式表示。

2、求解递归方程：使用数学方法（如主定理、迭代法、递归树等）求解递归方程。

3、考虑初始条件和边界情况：递归终止的条件对时间复杂度有重要影响。

常见递归算法及其时间复杂度

以下是一些常见递归算法及其时间复杂度的分析：

算法名称	递归关系	时间复杂度
阶乘	T(n) = T(n-1) + O(1)	O(n)
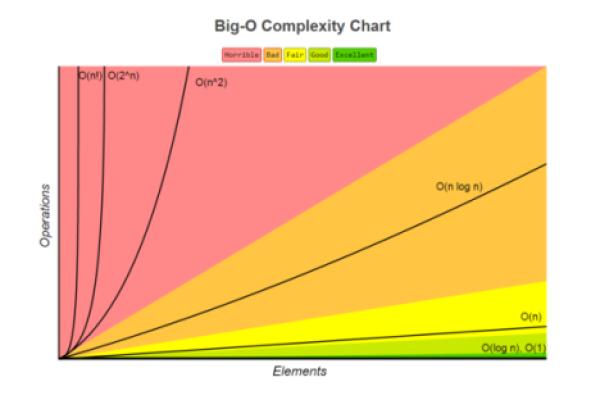
斐波那契序列	T(n) = T(n-1) + T(n-2)	O(2^n)
二分查找	T(n) = T(n/2) + O(1)	O(log n)
快速排序	T(n) = T(k) + T(n-k-1) + O(n)	O(n log n) (平均情况)
归并排序	T(n) = 2T(n/2) + O(n)	O(n log n)

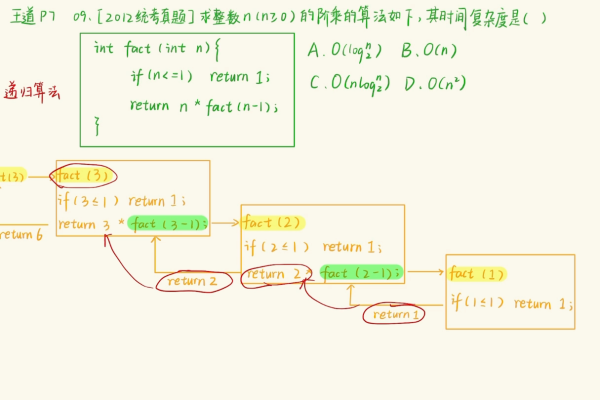
阶乘的时间复杂度分析

阶乘函数f(n) = n!可以通过递归定义为f(n) = n * f(n-1)，其中f(0) = 1，这个递归关系可以表示为T(n) = T(n-1) + O(1)，这是一个线性递归关系，通过迭代法可以得出其时间复杂度为O(n)。

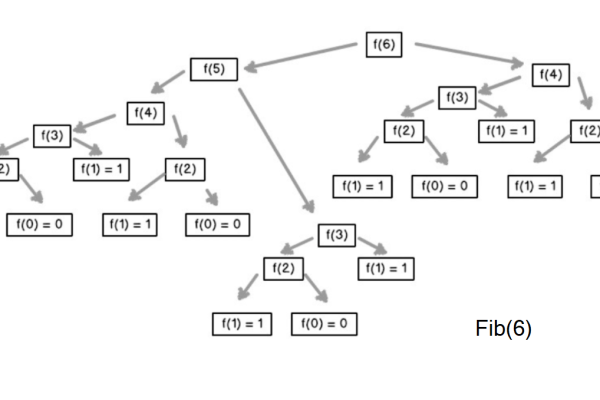
斐波那契序列的时间复杂度分析

斐波那契序列定义为F(n) = F(n-1) + F(n-2)，其中F(0) = 0, F(1) = 1，这个递归关系可以表示为T(n) = T(n-1) + T(n-2)，由于每个子问题都依赖于两个更小的子问题，这导致了指数级的增长，其时间复杂度为O(2^n)。

二分查找的时间复杂度分析

二分查找算法每次将搜索区间减半，因此递归关系为T(n) = T(n/2) + O(1)，这是一个对数级的递归关系，其时间复杂度为O(log n)。

快速排序的时间复杂度分析

快速排序的平均时间复杂度分析较为复杂，因为它依赖于分区的选择，在最佳情况下，分区均匀，递归关系为T(n) = T(k) + T(n-k-1) + O(n)，其中k约为n/2，通过主定理可以得出其平均时间复杂度为O(n log n)。

归并排序的时间复杂度分析

归并排序的递归关系为T(n) = 2T(n/2) + O(n)，这也是一个对数级的递归关系，其时间复杂度为O(n log n)。

FAQs

Q1: 为什么斐波那契序列的时间复杂度是O(2^n)？

A1: 斐波那契序列的递归关系导致每个子问题都依赖于两个更小的子问题，这形成了指数级的增长，计算F(n)需要计算F(n-1)和F(n-2)，而计算F(n-1)又需要计算F(n-2)和F(n-3)，以此类推，这种依赖关系导致了总的计算次数呈指数增长，因此时间复杂度为O(2^n)。

Q2: 如何优化斐波那契序列的递归算法？

A2: 斐波那契序列的递归算法可以通过多种方式进行优化，例如使用动态规划、记忆化递归或者矩阵快速幂，动态规划通过存储已经计算过的值来避免重复计算，从而将时间复杂度降低到O(n)，记忆化递归结合了递归和动态规划的优点，使用一个数组来存储已经计算过的值，同样可以达到O(n)的时间复杂度，矩阵快速幂则利用了斐波那契数列的线性递归性质，通过矩阵运算来快速计算高次幂，也可以达到O(log n)的时间复杂度。

各位小伙伴们，我刚刚为大家分享了有关“递归的时间复杂度”的知识，希望对你们有所帮助。如果您还有其他相关问题需要解决，欢迎随时提出哦！