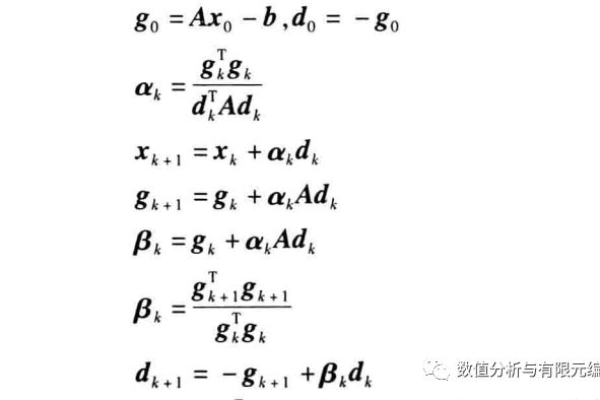高斯若尔当消元法求逆矩阵,逆矩阵高斯消元法(高斯消元法求矩阵的逆矩阵)
- 行业动态
- 2024-04-21
- 4833
高斯若尔当消元法求逆矩阵是一种常用的求解线性方程组的方法,其基本思想是通过行变换将线性方程组的增广矩阵化为阶梯形矩阵,然后通过回代求解未知数,在这个过程中,我们可以顺便求出原矩阵的逆矩阵,下面是详细的步骤:
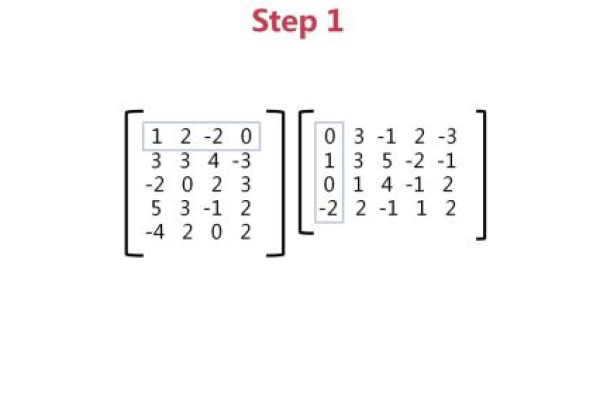
1、将线性方程组写成增广矩阵的形式:
假设我们有一个线性方程组:
a11x1 + a12x2 = b1
a21x1 + a22x2 = b2
…
an1x1 + an2x2 = bn
将其写成增广矩阵的形式:
M = | a11 a12 | | b1 |
| a21 a22 | | b2 |
…
| an1 an2 | | bn |
| 0 | | 1 |
2、对增广矩阵进行行变换,化为阶梯形矩阵:
我们将第一行乘以一个非零常数k,使得第一列的元素为0:
k * (a11 x1 + a12 x2) = k * b1
k * a11 = b1 / a12
x1 = b1 / (a12 * k)
x2 = (b2 a21 * x1) / a22
我们将第二行减去第一行的倍数,使得第二列的元素为0:
(a21 k * a11) x1 + (a22 k * a12) x2 = b2 k * b1
(a21 k * a11) x1 = b2 k * b1 (a22 k * a12) x2
x1 = (b2 k * b1 (a22 k * a12) x2) / (a21 k * a11)
x2 = …
重复这个过程,直到所有行都化为阶梯形矩阵。
3、从最后一个非零行开始,依次回代求解未知数:
对于最后一个非零行(第n行),我们可以直接求解xn:
xn = (bn an1 * xn1 an2 * xn2) / (an3 an1 * an2 * xn3)
对于倒数第二个非零行(第n1行),我们可以通过以下公式求解xn1:
xn1 = (b(n1) an(n1) * xn) / (an(n+1) an(n1) * an(n))
以此类推,直到求解出第一个未知数x1。
4、计算逆矩阵:
在求解过程中,我们可以得到一个与增广矩阵M相似的矩阵N(除了最后一列是单位向量外),原矩阵A的逆矩阵A^1就是N的逆矩阵N^1,由于N的最后一列是单位向量,所以N^1的最后一列也是单位向量,我们只需要计算N的前n1列的逆矩阵即可。
本站发布或转载的文章及图片均来自网络,其原创性以及文中表达的观点和判断不代表本站,有问题联系侵删!
本文链接:http://www.xixizhuji.com/fuzhu/225849.html