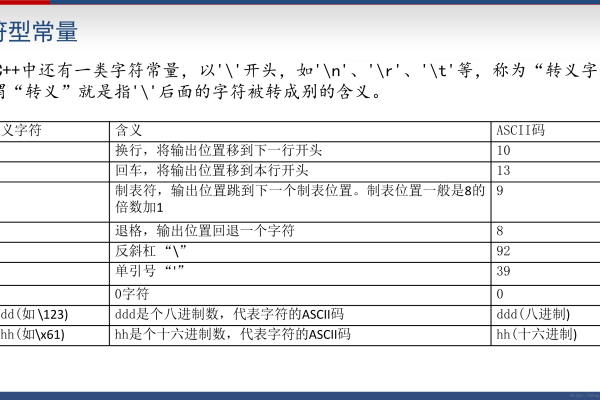
实型常量是什么?
- 行业动态
- 2024-10-30
- 3617
实型常量是编程中用于表示带有小数部分的数值,如3.14或0.5。
在计算机科学和编程中,实型常量(Real Constant)是指那些表示浮点数的数值,与整数常量不同,实型常量可以包含小数部分,因此能够表示更精确的数值,实型常量通常用于需要高精度计算的场景,如科学计算、工程模拟、金融分析等领域。

实型常量的表示
实型常量可以通过多种方式表示,具体取决于所使用的编程语言或环境,以下是一些常见的表示方法:
1、十进制表示:这是最常见的表示方法,直接使用小数形式表示数值,3.14、0.001等。
2、科学记数法:对于非常大或非常小的数值,可以使用科学记数法表示,1.23e4表示12300,而4.56e-3表示0.00456。
3、十六进制表示:在某些编程语言中,也可以使用十六进制表示实型常量,0x1.8p+1表示十进制的3.14。
实型常量的类型
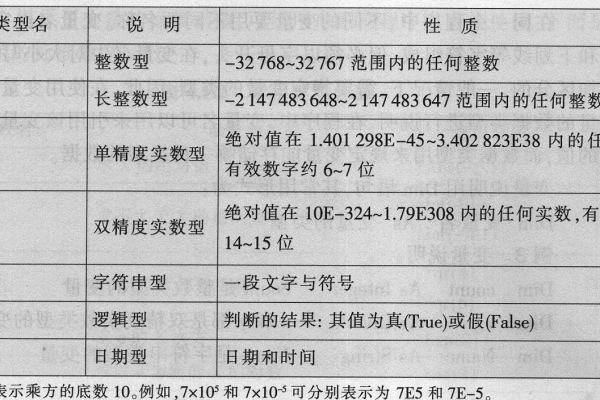
根据精度和存储方式的不同,实型常量可以分为以下几种类型:
1、单精度浮点数:通常占用4个字节(32位),包括1位符号位、8位指数位和23位尾数位,单精度浮点数的精度较低,但占用空间较小,适合对精度要求不高的场合。
2、双精度浮点数:通常占用8个字节(64位),包括1位符号位、11位指数位和52位尾数位,双精度浮点数的精度较高,但占用空间较大,适合对精度要求较高的场合。
3、扩展精度浮点数:在某些高级语言或库中,还支持扩展精度浮点数,如C++中的long double类型,扩展精度浮点数通常占用更多字节,提供更高的精度,但计算速度可能较慢。
实型常量的应用
实型常量在各种领域都有广泛的应用,以下是一些典型的例子:
1、科学计算:在物理、化学、生物等自然科学领域,实型常量用于表示测量结果、实验数据等,光速约为299,792,458米/秒,万有引力常数约为6.67430 × 10^-11 N(m²/kg²)。
2、工程模拟:在机械、电子、土木等工程领域,实型常量用于表示设计参数、材料属性等,钢材的弹性模量约为200 GPa,混凝土的抗压强度约为30 MPa。
3、金融分析:在经济、金融等领域,实型常量用于表示利率、汇率、股票价格等,一年期存款利率为1.5%,美元兑人民币的汇率为6.5。
实型常量的注意事项
在使用实型常量时,需要注意以下几点:
1、精度问题:由于计算机内部采用二进制表示数值,某些十进制小数无法精确表示为二进制小数,因此在进行浮点数运算时可能会出现精度损失,为了避免这种情况,可以使用高精度库或算法来提高计算精度。
2、舍入误差:在进行多次浮点数运算时,舍入误差可能会累积,导致最终结果与预期值有较大偏差,为了减少舍入误差的影响,可以适当调整计算顺序或使用其他数学技巧。
3、溢出和下溢:当实型常量的数值超出其表示范围时,会发生溢出或下溢现象,为了避免这种情况,可以根据实际需求选择合适的浮点数类型和范围。
相关问答FAQs
Q1: 为什么有时候打印出来的浮点数与输入的值不完全相同?
A1: 这是因为计算机内部使用二进制表示数值,某些十进制小数无法精确地转换为二进制小数,在打印或显示浮点数时,可能会出现精度损失的情况,为了解决这个问题,可以使用格式化输出函数来控制显示的精度。
Q2: 如何选择合适的浮点数类型?
A2: 选择合适的浮点数类型主要取决于实际需求和应用场景,如果对精度要求不高且希望节省内存空间,可以选择单精度浮点数;如果对精度要求较高且可以接受较大的内存开销,则应选择双精度浮点数;对于极端情况下的高精度需求,可以考虑使用扩展精度浮点数或其他高精度库。
本站发布或转载的文章及图片均来自网络,其原创性以及文中表达的观点和判断不代表本站,有问题联系侵删!
本文链接:http://www.xixizhuji.com/fuzhu/108855.html