如何将CDN文件上传至ECS?
- 行业动态
- 2024-12-17
- 6
如何将CDN文件上传到ECS
一、选择合适的CDN提供商
1、评估需求:在选择CDN提供商之前,需要明确网站或应用的流量大小、目标用户所在区域、需要加速的内容类型(如视频、图片、文件等)以及预算,这些因素有助于缩小选择范围,找到最合适的CDN解决方案。
2、比较不同CDN提供商:市面上有许多知名的CDN提供商,如Cloudflare、Akamai、Amazon CloudFront、Microsoft Azure CDN等,可以根据价格、地理覆盖范围、技术支持、易用性和性能等因素进行比较。
二、创建和配置CDN账户
1、注册账户:一旦选择了合适的CDN提供商,下一步是注册一个账户,大多数CDN提供商都提供免费试用期,可以先注册试用账户,测试其性能和功能。
2、配置CDN服务:注册成功后,登录到CDN提供商的管理控制台,按照以下步骤配置CDN服务:
创建CDN分发:在控制台中创建一个新的CDN分发(Distribution),并选择需要加速的内容类型(如静态文件、视频流等)。
设置源服务器:配置源服务器(Origin Server),即存储原始文件的服务器地址,当CDN节点没有缓存请求的内容时,会从源服务器获取。
配置缓存规则:设置缓存规则,包括缓存时间、缓存策略等,合理的缓存设置可以提高内容分发的效率。
配置SSL证书:如果需要加速HTTPS内容,配置SSL证书以确保数据传输的安全性。
配置域名:将域名(如example.com)与CDN分发关联,这样用户访问域名时,流量会自动路由到CDN节点。
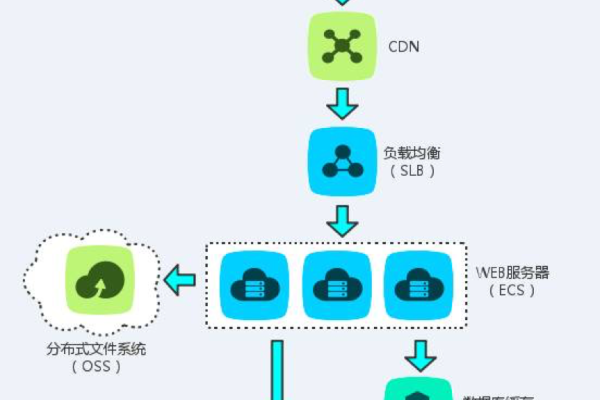
三、上传文件到源服务器
1、选择上传方式:将文件上传到源服务器有多种方式,可以选择适合自己的方式进行操作:
FTP/SFTP:通过FTP或SFTP客户端将文件上传到源服务器,这种方式适合上传大批量文件。
Web界面:有些源服务器提供Web界面,可以通过浏览器直接上传文件。
API:如果需要自动化上传文件,可以使用API接口进行操作,大多数源服务器和CDN提供商都提供API文档。
2、组织文件结构:在上传文件之前,建议先整理好文件结构,以便后续管理和访问,可以按照文件类型、日期等进行分类存放。
四、配置CDN服务
1、设置缓存策略:合理的缓存策略可以显著提高CDN的性能和效率,常见的缓存策略包括:
静态文件缓存:设置较长的缓存时间(如30天或更长),适用于图片、CSS、JS等不频繁更新的文件。
动态文件缓存:设置较短的缓存时间(如几分钟或几小时),适用于频繁更新的内容,如新闻、博客文章等。
缓存清理:当源服务器上的文件更新时,可以通过CDN提供商的控制台或API接口清理缓存,确保用户获取到最新的内容。
2、设置安全策略:为了保护内容和用户数据,建议配置以下安全策略:
SSL/TLS:启用SSL/TLS加密,确保数据在传输过程中不被窃取或改动。
防盗链:通过配置防盗链策略,防止其他网站未经授权直接引用资源。
DDoS防护:选择具备DDoS防护功能的CDN服务,防止反面攻击导致服务中断。
五、测试和验证
1、性能测试:在配置完成后,建议对CDN服务进行性能测试,确保其能够满足需求,可以使用一些性能测试工具,如Pingdom、GTmetrix等,测试页面加载速度、响应时间等指标。
2、功能验证:除了性能测试外,还需要验证CDN服务的各项功能是否正常工作,如缓存策略、SSL/TLS配置、防盗链等,可以通过手动测试或编写自动化测试脚本进行验证。
六、监控和优化
1、实时监控:为了确保CDN服务的稳定性和可靠性,建议启用实时监控功能,大多数CDN提供商都提供监控工具,可以监控流量、请求数、缓存命中率、错误率等指标。
2、定期优化:根据监控数据,定期对CDN服务进行优化,如果发现某些文件的缓存命中率较低,可以调整缓存策略;如果某些区域的用户访问速度较慢,可以考虑增加该区域的CDN节点等。
七、常见问题及解决方案
1、缓存未命中:如果发现CDN缓存未命中率较高,可能是缓存策略设置不合理,或源服务器响应时间较长,可以尝试调整缓存策略,增加缓存时间,或优化源服务器的性能。
2、SSL/TLS配置问题:如果在配置SSL/TLS时遇到问题,可以检查证书是否正确安装,域名是否正确配置,或联系CDN提供商的技术支持寻求帮助。
3、防盗链失效:如果防盗链策略失效,可能是配置错误或规则设置不当,可以重新检查防盗链配置,确保规则正确无误。
八、使用案例
1、电商网站:某大型电商网站使用CDN服务加速其静态资源(如图片、CSS、JS等)的加载速度,并通过配置缓存策略和SSL/TLS加密,确保用户数据的安全性,通过CDN服务,该网站的页面加载速度提高了30%,用户体验显著提升。
2、视频平台:某视频平台使用CDN服务加速视频流的传输,通过选择在目标用户区域有强大节点覆盖的CDN提供商,确保视频播放的流畅性和稳定性,通过配置DDoS防护策略,防止反面攻击导致服务中断。
3、新闻网站:某新闻网站使用CDN服务加速其动态内容的分发,通过设置合理的缓存策略,确保用户能够快速获取最新的新闻内容,通过监控和优化CDN服务,提升了网站的整体性能和可靠性。
九、未来发展趋势
1、边缘计算:随着边缘计算的发展,CDN服务将逐渐融合边缘计算技术,通过在用户附近的节点处理和缓存内容,进一步提高内容分发的效率和响应速度。
2、人工智能:人工智能技术将被广泛应用于CDN服务,如通过机器学习算法优化缓存策略、预测流量峰值等,从而提升CDN服务的智能化和自动化水平。
3、多云CDN:多云CDN将成为一种趋势,通过集成多个云服务提供商的CDN服务,提供更广泛的地理覆盖范围和更高的冗余性,确保内容分发的稳定性和可靠性。
将文件上传到CDN是一个系统化的过程,需要选择合适的CDN提供商、配置账户、上传文件、设置缓存和安全策略、进行测试和优化等多个步骤,通过合理的配置和管理,可以显著提升网站或应用的性能和用户体验。
小伙伴们,上文介绍了“cdn文件上传ecs”的内容,你了解清楚吗?希望对你有所帮助,任何问题可以给我留言,让我们下期再见吧。