如何选择和购买适合的ASP中间件产品?
- 行业动态
- 2024-11-28
- 2101
在当今的软件开发领域,中间件扮演着至关重要的角色,尤其是在构建基于ASP(Active Server Pages)的应用时,ASP是微软推出的一种服务器端脚本环境,用于生成动态网页和Web应用程序,为了增强ASP应用的功能和性能,开发者往往需要购买和使用各种中间件产品,本文将探讨ASP环境下常用的中间件类型、购买考虑因素以及如何选择合适的中间件来优化您的ASP项目。
中间件的重要性与作用
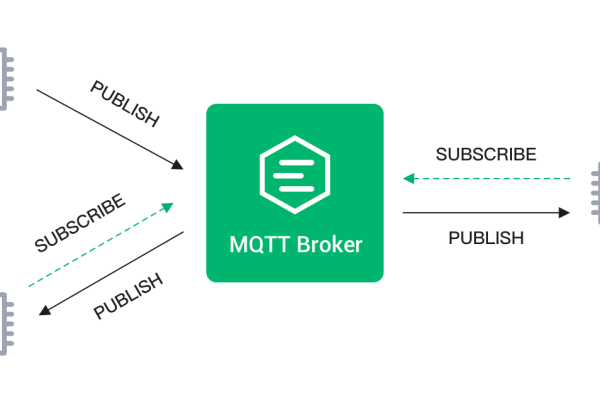
中间件可以视为连接不同软件组件或系统的桥梁,它处理客户端请求,执行业务逻辑,并与数据库或其他服务交互,在ASP环境中,合适的中间件能够提升数据处理效率,增强安全性,简化开发流程,并提供更好的扩展性和维护性,消息队列中间件帮助异步处理任务,而缓存中间件则能显著提高数据检索速度。
常见的ASP中间件类型
| 类别 | 功能描述 | 示例产品 |
| 数据库访问 | 提供高效的数据库连接和查询执行能力 | ADO.NET, Dapper, Entity Framework |
| 缓存 | 存储频繁访问的数据以提高响应速度 | Memcached, Redis |
| 消息队列 | 实现异步通信和解耦系统组件 | RabbitMQ, Apache Kafka |
| 日志管理 | 记录系统活动,便于监控和调试 | Log4Net, Serilog |
| Web服务框架 | 简化Web API的开发和部署 | .NET Core, NancyFX |
| 安全认证 | 确保应用程序的安全性,管理用户身份验证 | OAuth2, OpenID Connect |
| 文件处理 | 高效地读写和管理文件系统资源 | SharpZipLib, NPOI (Excel处理) |
购买中间件时的考量因素
1、兼容性:确保所选中间件与现有的ASP版本及操作系统兼容。
2、性能:评估中间件的性能指标,如处理速度、吞吐量等。
3、可扩展性:考虑未来业务增长,选择能够轻松扩展的中间件解决方案。
4、社区支持与文档:强大的社区支持和详细的文档可以帮助快速解决问题。
5、成本效益:分析总体拥有成本,包括许可费、培训费用及维护开支。
6、安全性:检查中间件的安全特性,确保符合行业标准和合规要求。
如何选择适合的中间件
明确需求:首先确定您的ASP应用具体需要哪些功能增强或性能优化。
市场调研:研究市场上可用的中间件选项,对比其特点和评价。
试用与测试:利用免费试用版或开源替代方案进行实际测试,验证其效果。
咨询专家:向同行或专业顾问咨询意见,特别是那些有类似项目经验的人。
长期规划:考虑中间件的未来发展方向和技术趋势,避免短期内再次更换。
相关问答FAQs
Q1: ASP应用中引入中间件会增加多少成本?
A1: 成本取决于所选中间件的类型、许可模式以及是否已有相应的基础设施支持,开源中间件通常成本较低,但可能需投入更多时间进行定制和集成;商业中间件虽初期投入较高,但往往提供更完善的技术支持和服务,综合考虑直接费用与间接效益后做出决策。
Q2: 如何评估中间件对现有ASP应用的影响?
A2: 评估影响应从多个维度进行,包括但不限于性能测试(如响应时间和资源消耗)、兼容性检查、安全性审计以及用户体验反馈,实施前进行全面的测试,并准备回滚计划以应对可能出现的问题,监控中间件运行状况,及时调整配置以优化性能和稳定性。
以上就是关于“asp 购买中间件”的问题,朋友们可以点击主页了解更多内容,希望可以够帮助大家!
本站发布或转载的文章及图片均来自网络,其原创性以及文中表达的观点和判断不代表本站,有问题联系侵删!
本文链接:http://www.xixizhuji.com/fuzhu/96593.html