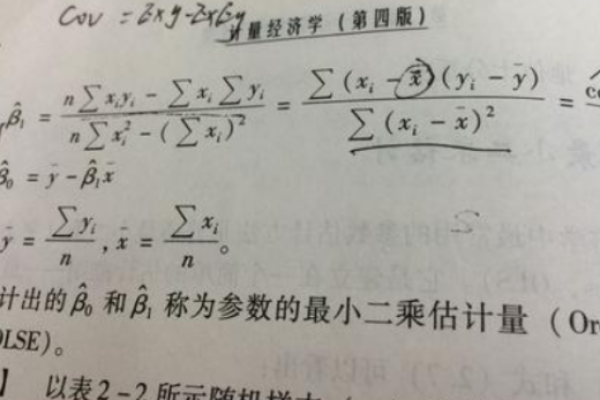MySQL中如何实现最小二乘法的计算?
- 行业动态
- 2024-09-30
- 4584
MySQL中没有直接的最小二乘法函数,但可以使用SQL语句和数学公式实现。
在MySQL中,最小二乘法是一种常用的统计方法,用于数据拟合和回归分析,通过编写函数或存储过程,可以实现最小二乘法的计算。

什么是最小二乘法
最小二乘法(Least Squares Method)是一种数学优化技术,旨在通过最小化误差的平方和来寻找数据的最佳函数匹配,其基本思想是:给定一组数据点,找到一个函数,使得函数预测值与实际观测值之间的差的平方和最小,这种方法广泛应用于统计学中的线性回归分析。
最小二乘法的数学公式
对于一元线性回归(y = ax + b),最小二乘法的目标是找到参数a(斜率)和b(截距),使得误差平方和最小:
[ S = sum_{i=1}^{n} (y_i (ax_i + b))^2 ]
通过对S关于a和b求偏导并使其等于零,可以得到一个线性方程组,解这个方程组即可得到最优的a和b。
MySQL实现最小二乘法步骤
1. 创建数据库和表
创建一个包含最小二乘法所需数据的数据库和表,假设有一个名为least_squares的表,其中包含id、x和y字段。
CREATE DATABASE least_squares_db;
USE least_squares_db;
CREATE TABLE least_squares (
id INT PRIMARY KEY AUTO_INCREMENT,
x FLOAT NOT NULL,
y FLOAT NOT NULL
);2. 插入数据
向表中插入一些示例数据。
INSERT INTO least_squares (x, y) VALUES (1, 2), (2, 3), (3, 5), (4, 4), (5, 6);
3. 定义存储过程
编写一个存储过程来计算最小二乘法的斜率和截距。
DELIMITER //
CREATE PROCEDURE calculate_least_squares()
BEGIN
DECLARE x_sum FLOAT;
DECLARE y_sum FLOAT;
DECLARE xy_sum FLOAT;
DECLARE x_squared_sum FLOAT;
DECLARE n INT;
DECLARE slope FLOAT;
DECLARE intercept FLOAT;
SELECT COUNT(*) INTO n FROM least_squares;
SELECT SUM(x) INTO x_sum FROM least_squares;
SELECT SUM(y) INTO y_sum FROM least_squares;
SELECT SUM(x * y) INTO xy_sum FROM least_squares;
SELECT SUM(x * x) INTO x_squared_sum FROM least_squares;
SET slope = (n * xy_sum x_sum * y_sum) / (n * x_squared_sum x_sum * x_sum);
SET intercept = (y_sum slope * x_sum) / n;
SELECT slope AS 'Slope', intercept AS 'Intercept';
END //
DELIMITER ;4. 调用存储过程
执行存储过程以计算斜率和截距。
CALL calculate_least_squares();
5. 结果展示
存储过程执行后,将返回最小二乘法计算出的斜率和截距,这些结果可以用于进一步的数据分析或可视化展示。
FAQs
1. 如何更新数据并重新计算?
你可以通过插入新数据或更新现有数据来更新表中的数据,然后再次调用存储过程进行计算。
2. 是否可以处理多元回归?
是的,可以通过扩展存储过程来处理多元回归问题,需要增加更多的变量和计算步骤。
3. 如何处理非线性数据?
对于非线性数据,可以考虑使用多项式回归或其他非线性回归模型,这通常需要更复杂的数学公式和计算方法。
4. 如何验证结果的准确性?
你可以使用已知数据集来验证计算结果的准确性,还可以将MySQL的结果与其他统计软件(如R、Python等)的结果进行比较。
5. 是否有性能优化的建议?
对于大型数据集,可以考虑使用索引来加快查询速度,还可以考虑使用分区表或分布式计算来提高性能。
通过以上步骤,你可以在MySQL中实现最小二乘法的计算,并通过编写存储过程来自动化整个过程,希望这些信息对你有所帮助!
本站发布或转载的文章及图片均来自网络,其原创性以及文中表达的观点和判断不代表本站,有问题联系侵删!
本文链接:http://www.xixizhuji.com/fuzhu/81162.html