如何有效利用MATLAB进行卷积操作？

MATLAB卷积用户指南提供了关于如何在MATLAB中执行卷积操作的详细指导。它解释了卷积的基本概念，展示了如何使用内置函数进行一维和二维卷积，并提供了示例代码来帮助用户理解和应用卷积在信号处理和图像处理中的应用。

在数字信号处理领域，卷积是一种基本且重要的数学运算，MATLAB作为一种广泛使用的科学计算软件，提供了强大的函数和工具箱支持卷积运算，了解如何在MATLAB中有效执行卷积运算对于科研人员和工程师至关重要，本文旨在全面介绍MATLAB中的卷积操作，从基础概念到高级应用，帮助用户深入理解并高效利用卷积功能。

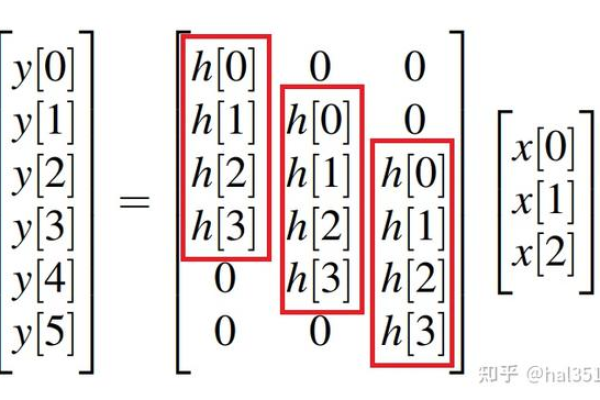
卷积基础

卷积在信号处理中用于描述一个信号如何通过线性系统，在MATLAB中，卷积可以通过内置的conv函数实现，该函数接受两个向量作为输入，分别代表两个信号，并输出它们的卷积结果，对两个时间序列信号进行卷积，可以按照如下步骤进行：

1、定义时间范围和信号：

“`matlab

t=1:0.01:5;

f1=((t>0)(t>3));

f2=exp(t).*(t>0);

“`

2、使用conv函数计算卷积：

“`matlab

f3=conv(f1,f2); f3=f3*0.01;

“`

3、确定结果的时间范围：

“`matlab

k=2*length(t)1;

“`

高级卷积技巧

对于更复杂的信号或大型数据集，可以使用MATLAB的高级卷积技术来提升性能，并行卷积计算可以显著提高大型图像或信号的处理速度，使用parfor循环或spmd块，可以在MATLAB中实现并行卷积，这种并行处理策略尤其适用于处理高分辨率图像或长时间序列数据。

MATLAB还提供了多种卷积核供选择，如平均滤波器、高斯滤波器等，这些可以通过fspecial函数生成，选择合适的卷积核对于达到期望的信号处理效果至关重要。

性能优化

在实际应用中，优化卷积性能是提高效率的关键，除了使用并行计算外，MATLAB还允许用户自定义卷积算法，例如利用快速傅里叶变换（FFT）进行频域卷积，这通常比直接时域卷积更快，通过fft和ifft函数，可以轻松实现这一转换：

F1 = fft(f1);
F2 = fft(f2);
F3 = F1 .* F2;
f3 = ifft(F3);

应用案例

卷积在多个领域内有着广泛的应用，包括图像处理、音频信号处理和系统分析等，在图像处理中，卷积常用于图像平滑、锐化及特征提取，在MATLAB中，可以方便地应用不同的卷积核对图像进行处理：

I = imread('image.jpg');
h = fspecial('average', 3);
J = conv2(double(I), h, 'same');

这里使用了平均滤波器来平滑图像，通过简单地更改fspecial的参数，可以实现不同的图像处理效果。

上文归纳性指导

为了最大化MATLAB中卷积的性能，建议采用以下策略：

根据数据的规模和复杂度选择合适的卷积方法；

利用MATLAB的并行计算工具加速处理过程；

熟悉不同的卷积核及其应用场景；

掌握频域卷积技术以提高大规模数据处理的效率。

FAQs

Q1: MATLAB中的卷积结果时间范围是如何确定的？

A1: 卷积结果的时间范围是由输入信号的时间范围决定的，结果的最大长度为两个输入信号长度之和减一。

Q2: 如何使用MATLAB进行三维数据的卷积？

A2: 在MATLAB中，可以使用convn函数对多维数据执行卷积，对于一个三维数组，可以使用类似convn(A, B, 'same')的语法进行卷积操作，其中A和B是三维数组。

通过以上内容，用户可以详细了解MATLAB中卷积的操作方法和应用技巧，从而有效地利用MATLAB进行科研或工程中的信号处理任务。