Vue.js CDN加速实践,如何优化加载速度?
- 行业动态
- 2025-03-10
- 6
一、CDN加速
1、定义:
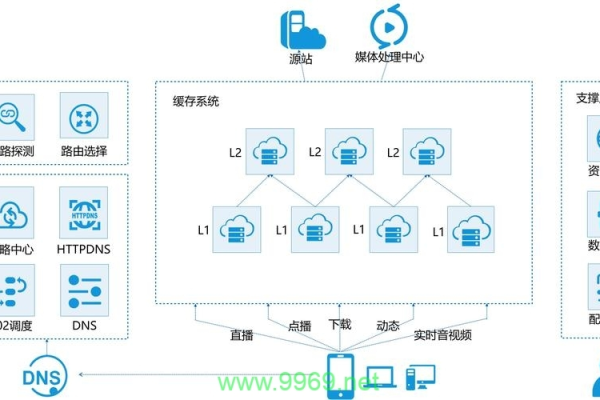
CDN(Content Delivery Network,内容分发网络)是一种分布式网络服务,它通过在地理上分散的多个服务器上存储内容的副本,使用户可以从最近的服务器节点获取数据,从而加快内容的加载速度和提高可用性。
2、原理:
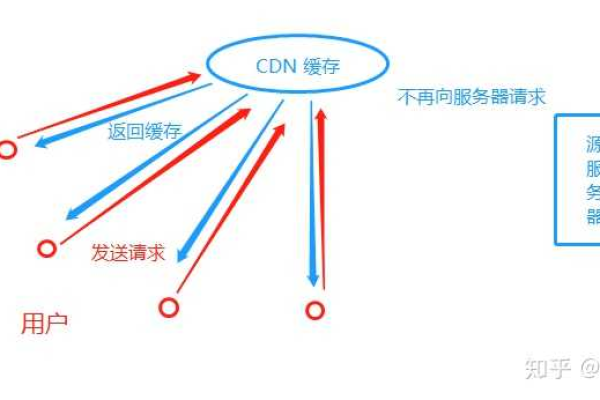
当用户请求某个资源时,CDN会根据用户的地理位置、网络条件等因素,智能地选择距离用户最近或负载最轻的服务器节点来响应请求,减少数据传输延迟,提高访问速度。
3、优势:
提高加载速度:通过将静态资源缓存到离用户更近的节点,减少了资源的传输时间,显著提升页面加载速度。
减轻服务器负担:部分请求由CDN节点处理,减轻了源服务器的压力,提高了系统的整体性能和稳定性。
提高可用性:即使源服务器出现故障或遭受攻击,CDN节点仍可继续提供服务,确保网站的高可用性。
二、Vue.js项目中使用CDN加速的步骤
1、查看依赖版本:
记录项目中需要使用CDN加速的依赖项及其版本号,如果项目中使用了vue、vuex、vue-router等依赖,需要明确它们的版本号。
2、配置开发和生产环境入口:
在Vue.js项目中,通常需要区分开发环境和生产环境的配置文件,可以创建main-dev.js作为开发环境入口文件,main-prod.js作为生产环境入口文件,并在其中引用相应的依赖。
3、修改vue.config.js:
在vue.config.js文件中,通过配置externals选项来排除不需要打包进项目的依赖项,对于vue、axios等依赖,可以在生产环境下将其排除。
根据需要配置publicPath属性,将其设置为CDN加速域名。
4、查找CDN地址:
可以通过多种方式查找CDN地址,如通过官方网站(如Bootstrap中文网、cdnjs官网等)查找最新版本的资源URL。
注意选择适合项目需求的版本,并确保引入的CSS、JS和Map文件完整且正确。
5、在项目中使用CDN链接:
将查找到的CDN链接复制到项目的相应位置,在index.html中通过<script>标签引入CDN加速的JavaScript文件,在<head>中通过<link>标签引入CSS文件。
确保引入的顺序正确,避免依赖冲突。
6、验证配置效果:
完成上述步骤后,重新构建项目并部署到生产环境。
通过浏览器开发者工具检查网络请求,确认静态资源是否已通过CDN加速加载。
三、常见问题与解答
1、Q: 为什么需要对Vue.js项目进行CDN加速?
A: 对Vue.js项目进行CDN加速可以提高项目的加载速度和用户体验,通过将静态资源缓存到离用户更近的服务器节点上,减少了资源的传输时间,降低了服务器负担,并提高了系统的可用性和稳定性。
2、Q: 如何选择合适的CDN服务提供商?
A: 选择合适的CDN服务提供商需要考虑多个因素,包括价格、性能、可靠性、技术支持等,建议在选择前进行充分的市场调研和比较,选择信誉良好、服务质量高的CDN服务提供商,也可以考虑使用免费的CDN服务进行测试和评估。