CDN缓存数据，如何有效管理和利用缓存机制？

一、CDN缓存数据

1、定义：CDN（Content Delivery Network），即内容分发网络，是一种通过在多个地理位置分散的服务器上缓存网站资源的技术，当用户请求某个资源时，CDN会从距离用户最近的服务器提供该资源，从而提高访问速度和效率。

2、缓存规则：CDN节点在收到源站响应的静态文件资源时，会根据一系列规则来执行缓存，这些规则包括源站响应头信息中的Cache-Control和Expires字段，以及CDN控制台设置的缓存过期时间或状态码过期时间，如果源站响应头中包含Cache-Control: max-age指令，则CDN节点会按照该指令缓存文件；如果包含no-cache、no-store或max-age=0指令，则不缓存。

3、缓存更新机制：CDN缓存主要通过两种机制进行更新，一是当缓存超出过期时间时，CDN节点会向源站发起回源请求，验证缓存是否仍然有效，如果源站返回304状态码，表示内容未发生变化，CDN节点将仅更新缓存的有效周期，而不变更缓存内容；如果源站返回200状态码和更新后的内容，CDN节点将覆盖旧缓存并更新为新内容，二是当业务需要立即更新CDN上资源的缓存时，可以通过CDN控制台或API接口下发刷新任务，强制将CDN节点上的缓存刷新。

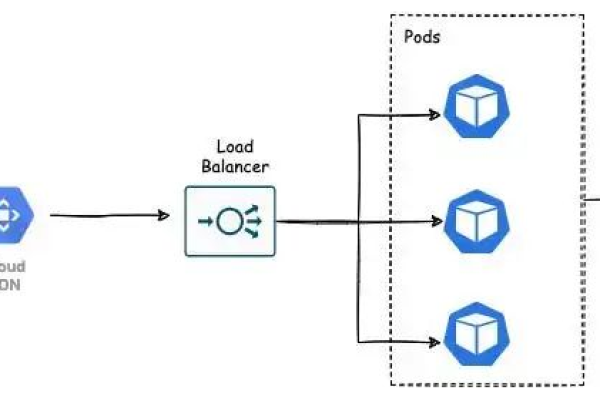
4、缓存优化策略：为了提升CDN缓存的利用率和性能，可以采取以下策略，一是根据业务场景对不同类型文件设置不同缓存规则，如对于不经常变化的文件设置较长缓存时间，而对于频繁更新的文件降低缓存时间，二是利用版本控制，在URL中添加版本号或哈希值，确保内容更新及时反映，三是监控缓存命中率和性能指标，及时发现并解决缓存问题。

二、相关问题与解答

1、问题：如何判断CDN缓存是否成功？

回答：可以通过检查HTTP响应头中的X-Cache字段来判断，如果值为HIT，则表示请求命中了CDN缓存；如果值为MISS或字段不存在，则表示请求没有命中缓存。

2、问题：如何解决URL的传递参数为变量导致CDN缓存命中率低的问题？

回答：可能是因为没有开启CDN的忽略参数功能，详情请参见相关文档或联系CDN服务提供商以获取更多信息。

3、问题：如何设置文件不缓存直接回源？

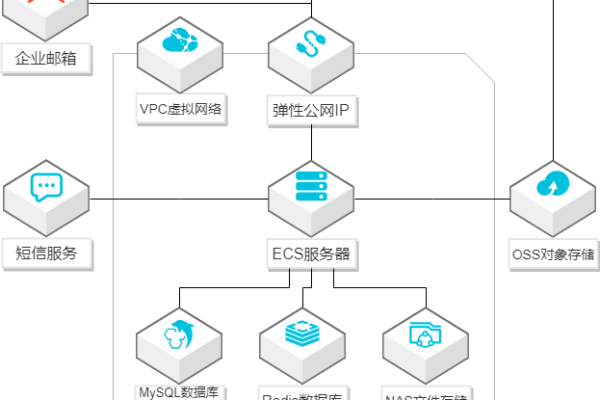
回答：针对不希望缓存的资源，可以按照目录、文件路径、文件类型设置对应的缓存时间，在CDN控制台中选择“不缓存”，并填写不想缓存的具体资源路径或文件名后缀，将过期时间设置为“0”，表示不缓存该类型的资源。