存储结构 数组
- 行业动态
- 2025-02-17
- 11
原理、特性与应用全解析
在计算机科学的数据存储领域,存储结构起着至关重要的作用,它决定了数据在计算机内存中的组织方式和存取方法,数组作为一种基础且常用的存储结构,具有独特的性质和广泛的应用场景。
一、数组的基本概念
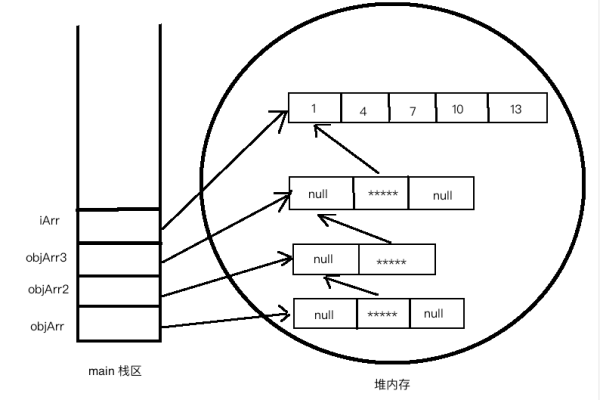
数组是一种线性存储结构,它将具有相同类型的多个数据元素依次存储在一块连续的内存空间中,这些元素在物理位置上是相邻的,并且可以通过一个统一的数组名和不同的下标来进行访问,在 C 语言中,声明一个整型数组int arr[5];,就表示在内存中分配了一块可以存储 5 个整型数据的连续空间,可以通过arr[0]、arr[1] 等下标来访问其中的每一个元素。
二、数组的存储方式
1、顺序存储
数组采用顺序存储的方式,即按照数据元素的逻辑顺序,将它们依次存放在一片连续的存储单元中,这种存储方式使得数组具有以下特点:
| 特点 | 描述 |
| 随机存取 | 由于每个元素在内存中的地址是连续的,可以通过计算得到任意元素的存储地址,从而实现对元素的快速随机访问,要访问数组arr 中的第i 个元素(假设数组基地址为LOC, 每个元素占用的存储单位大小为b),其地址计算公式为LOC + (i 1) * b,时间复杂度为O(1)。 |
| 存储密度高 | 由于没有额外的指针或链接等存储开销,数组的存储密度相对较高,能够有效地利用内存空间。 |
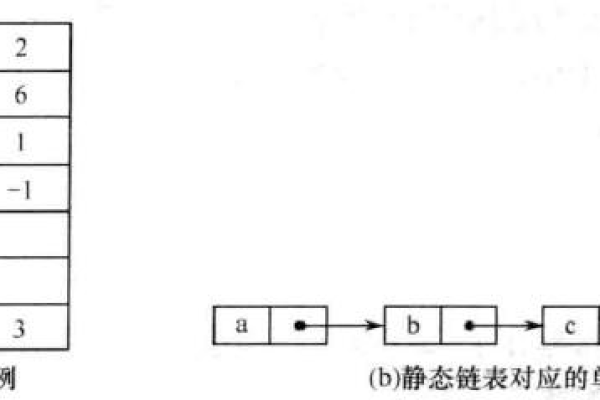
2、内存分配示例
以一个整型数组int arr[3] = {1, 2, 3}; 为例,假设整型数据在内存中占用 4 个字节,那么在内存中的存储情况可能如下表所示:
| 地址 | |
| 1000 | 1(整数 1 的二进制表示) |
| 1004 | 2(整数 2 的二进制表示) |
| 1008 | 3(整数 3 的二进制表示) |
三、数组的操作
1、插入操作
在数组的指定位置插入一个新元素时,需要将该位置及其后面的所有元素依次向后移动一位,以腾出空间来存放新元素,在一个长度为n 的数组arr 中插入一个新元素到位置i(0 <= i < n),时间复杂度为O(n i),因为从位置i 开始到数组末尾的所有元素都需要移动一位。
2、删除操作
删除数组中的某个元素时,同样需要将其后面的所有元素依次向前移动一位,以填补被删除元素留下的空位,删除数组arr 中位置i 的元素,时间复杂度为O(n i 1)。
3、查找操作
由于数组是随机存取的,查找特定位置的元素非常快,时间复杂度为O(1),但如果要查找满足某种条件的元素,可能需要遍历整个数组,时间复杂度为O(n)。
四、数组的应用
1、数据处理
数组常用于批量处理数据,如对一组学生的成绩进行统计分析、排序等操作,通过数组的下标可以方便地访问和操作每一个数据元素。
2、矩阵运算
在科学计算和图形学等领域,矩阵是一种常见的数据结构,而二维数组可以很好地表示矩阵,在图像处理中,一幅图像可以看作是一个由像素值组成的二维数组,通过对这个数组的操作可以实现图像的旋转、缩放、滤镜等效果。
五、FAQs
问题 1:为什么数组的大小在声明时通常需要确定?
答:因为在大多数编程语言中,数组采用静态内存分配方式,编译器需要在编译时就确定数组的大小,以便为其分配合适大小的连续内存空间,如果数组大小不确定,编译器无法准确地进行内存分配和管理,可能会导致内存错误或程序运行异常。
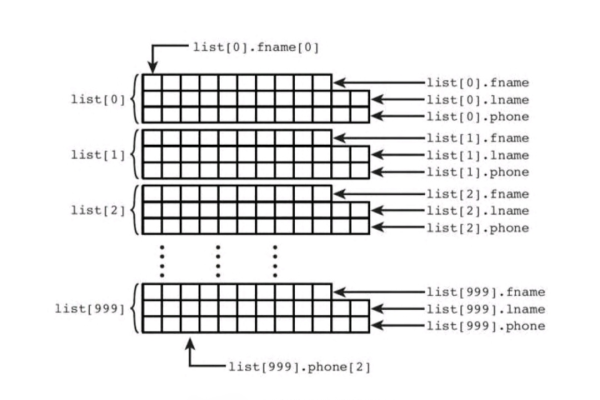
问题 2:数组和链表有什么区别?
答:数组和链表都是存储数据的结构,但它们在存储方式、访问方式和操作性能等方面存在差异,数组是顺序存储结构,元素在内存中连续存放,支持随机存取,访问速度快,但插入和删除操作可能导致大量元素移动,效率较低;链表是动态存储结构,元素在内存中不一定连续,通过指针链接,插入和删除操作方便灵活,只需要修改相关指针即可,但访问元素需要从头开始依次遍历,时间复杂度较高。
小编有话说
数组作为一种简单而有效的存储结构,在计算机科学和编程中有着不可替代的地位,它的顺序存储方式使得数据访问高效,但在插入和删除操作上存在一定的局限性,在实际开发中,我们需要根据具体的应用场景和需求,合理选择使用数组或其他数据结构,以达到最佳的程序性能和数据处理效果,对于数组的操作和使用,也需要深入理解其原理和特点,避免出现常见的错误和性能问题。