当前位置：首页 > 行业动态 > 正文

c哈夫曼数据结构

admin
行业动态
2025-02-20
4

哈夫曼数据结构是一种用于数据压缩的树形结构，通过构建二叉树实现最优前缀编码，使频繁元素用较短编码表示。

哈夫曼数据结构，即哈夫曼树（Huffman Tree），是一种广泛使用的带权路径长度最短的二叉树，常用于数据压缩和编码领域，以下是对哈夫曼数据结构的详细解释：

一、基本概念

1、定义：给定N个权值作为N个叶子节点，构造一棵二叉树，若该树的带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树（Huffman Tree）。

2、相关术语：

路径：从树中一个结点到另一个结点之间的分支构成这两个结点之间的路径。

路径长度：路径上的分支数目称作路径长度。

树的路径长度：从树根到每一结点的路径长度之和。

结点的带权路径长度：从该结点到树根之间的路径长度与结点上权的乘积。

树的带权路径长度（WPL）：树中所有叶子结点的带权路径长度之和，通常记作WPL。

c哈夫曼数据结构

二、构建过程

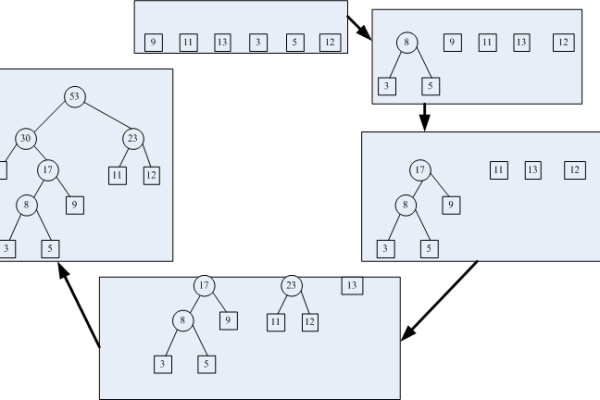
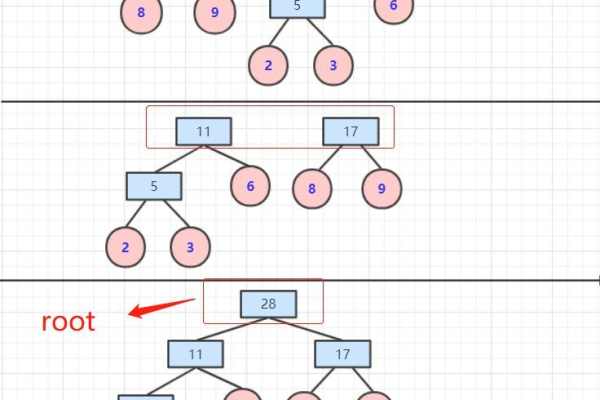
1、初始化：根据给定的n个权值{w1, w2, …, wn}，构造n棵只有根结点的二叉树，这些二叉树构成一个森林F。

2、选择合并：在森林F中选取两棵根结点的权值最小的树作为左右子树构造一棵新的二叉树，且置新的二叉树的根结点的权值为其左右子树上根结点的权值之和。

3、更新森林：在森林F中删除这两棵树，同时将新得到的二叉树加入F中。

4、重复步骤：重复上述两个步骤，直到F只含一棵树为止，这棵树便是哈夫曼树。

三、特点与优势

1、最优性：哈夫曼树是带权路径长度最短的二叉树，即它的WPL在所有可能的二叉树中是最小的。

c哈夫曼数据结构

2、前缀编码：哈夫曼树的每个字符编码都是唯一的，并且没有编码是其他编码的前缀，这种编码方式被称为前缀编码，它能够确保解码时不会产生二义性。

3、高效压缩：通过哈夫曼树，可以将频繁出现的字符用较短的编码表示，不常出现的字符用较长的编码表示，从而实现数据的高效压缩。

四、应用场景

1、数据压缩：哈夫曼树被广泛应用于数据压缩领域，如文件压缩、图像压缩、音频压缩等。

2、通信传输：在通信中，哈夫曼树可以用于信道编码，提高数据传输的效率和可靠性。

3、其他领域：除了数据压缩和通信传输外，哈夫曼树还可以应用于文本处理、信息检索等领域。

c哈夫曼数据结构

五、示例代码（Java实现）

以下是一个简单的Java实现示例，用于构建哈夫曼树并计算其带权路径长度（WPL）：

import java.util.*;
class HuffmanNode implements Comparable<HuffmanNode> {
    int weight;
    HuffmanNode left;
    HuffmanNode right;
    public HuffmanNode(int weight) {
        this.weight = weight;
    }
    @Override
    public int compareTo(HuffmanNode other) {
        return this.weight other.weight;
    }
}
public class HuffmanTree {
    public static void main(String[] args) {
        int[] weights = {5, 29, 7, 8, 14, 23, 3, 11}; // 示例权值
        PriorityQueue<HuffmanNode> queue = new PriorityQueue<>();
        // 初始化队列
        for (int weight : weights) {
            queue.add(new HuffmanNode(weight));
        }
        // 构建哈夫曼树
        while (queue.size() > 1) {
            HuffmanNode left = queue.poll();
            HuffmanNode right = queue.poll();
            HuffmanNode parent = new HuffmanNode(left.weight + right.weight);
            parent.left = left;
            parent.right = right;
            queue.add(parent);
        }
        // 输出哈夫曼树的带权路径长度（WPL）
        HuffmanNode root = queue.poll();
        int wpl = calculateWPL(root);
        System.out.println("哈夫曼树的带权路径长度（WPL）: " + wpl);
    }
    // 递归计算带权路径长度（WPL）
    private static int calculateWPL(HuffmanNode node) {
        if (node == null) {
            return 0;
        }
        return node.weight * getDepth(node) + calculateWPL(node.left) + calculateWPL(node.right);
    }
    // 获取节点深度（辅助函数）
    private static int getDepth(HuffmanNode node) {
        int depth = 0;
        while (node != null) {
            depth++;
            node = node.left != null ? node.left : node.right;
        }
        return depth 1;
    }
}