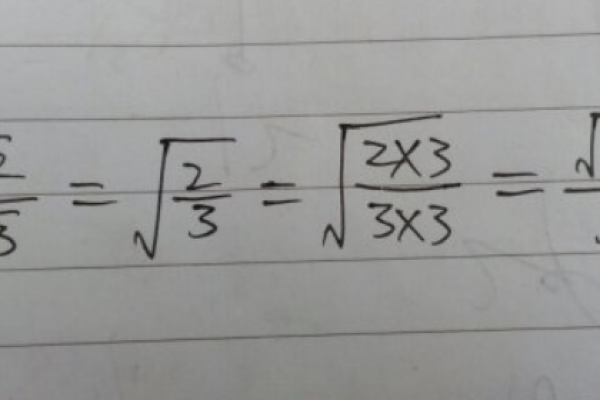根号符号的起源和演变是怎样的?
- 行业动态
- 2024-11-15
- 2863
根号符号(√)用于表示数学中的平方根,即一个数乘以自身等于另一个数时,后者的算术平方根。
在数学的广阔天地里,根号符号“√”扮演着一个独特而重要的角色,这个小小的符号,以其简洁的形式,蕴含着丰富的数学意义和应用,本文将深入探讨根号符号的历史、定义、性质以及它在各个领域中的应用,揭示这一符号背后的奥秘和价值。
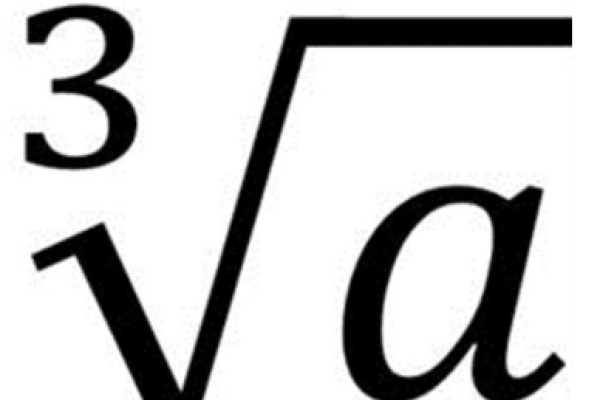
一、根号符号的起源与发展
根号符号“√”的起源可以追溯到古代文明时期,据史料记载,古巴比伦人早在公元前2000年左右就开始使用类似根号的符号来表示平方根运算,现代意义上的根号符号则源于16世纪中期的欧洲,当时,数学家们为了简化平方根运算的书写过程,开始采用缩写形式来表示平方根,并逐渐演变成了我们今天所熟知的根号符号“√”。
随着数学的发展,根号符号的应用范围不断扩大,从最初的平方根运算,到后来的立方根、四次方根等更高次方根运算,根号符号都发挥着不可或缺的作用,数学家们还根据实际需要,发展出了双根号(如√√)等变体形式,以满足更复杂的数学运算需求。
二、根号符号的定义与性质
1. 定义
根号符号“√”在数学中被定义为开方运算的符号,若a是一个非负数,则√a表示a的算术平方根,即满足x²=a的非负实数x,当a为正数时,其算术平方根唯一;当a为0时,其算术平方根为0;当a为负数时,其在实数范围内无算术平方根(但在复数范围内有定义)。
2. 性质
非负性:对于任何实数a,其算术平方根总是非负的。
唯一性:对于正数a,其算术平方根是唯一的。
乘法分配律:(√a)²=a,这是根号符号最基本的性质之一。
商的算术平方根:√(a/b)=√a/√b(b>0),这体现了根号符号在分数运算中的分配性。
最简二次根式:被开方数不含分母且被开方数中不含能开得尽方的因数或因式。
三、根号符号的应用
根号符号在数学领域有着广泛的应用,以下是一些常见的应用场景:
1. 代数运算
在代数运算中,根号符号常用于表示未知数的平方根,在求解一元二次方程ax²+bx+c=0(a≠0)时,我们可能需要用到根号符号来表示方程的解,在因式分解、分式运算等过程中,根号符号也经常被使用。
2. 几何问题
在几何学中,根号符号常用于表示线段的长度、面积的边长等,在勾股定理a²+b²=c²中,如果已知两条直角边的长度a和b,那么斜边c的长度就可以通过根号符号求得,在计算三角形的面积、圆的周长和面积等几何量时,根号符号也是不可或缺的工具。
3. 物理科学
在物理学和工程学等领域中,根号符号同样发挥着重要作用,在计算物体的加速度、速度、位移等物理量时,我们可能需要用到根号符号来表示这些量的平方根或立方根等,在电子电路分析、信号处理等领域中,根号符号也被广泛应用于各种计算公式和表达式中。
四、根号符号的拓展应用
除了上述传统应用领域外,根号符号还被拓展应用于计算机科学、经济学等多个领域,在计算机科学中,根号符号常用于算法设计、数据结构分析等方面;在经济学中,则可用于风险评估、投资组合优化等问题的解决,这些拓展应用进一步展示了根号符号的强大功能和广泛适用性。
五、FAQs
Q1: 如何手动计算一个数的平方根?
A1: 手动计算一个数的平方根可以通过多种方法实现,其中一种常用的方法是利用牛顿迭代法(也称为牛顿-拉弗森迭代法),该方法基于函数逼近原理,通过不断迭代逼近真实值,具体步骤如下:
1、选择一个初始猜测值x₀(通常可以选择被开方数的一半作为初始值)。
2、计算f(x) = x (x² a)/(2x),其中a为被开方数。
3、用新的猜测值x₁ = x₀ f(x₀)/f'(x₀)替换旧的猜测值x₀,其中f'(x)为f(x)的导数。
4、重复步骤2和3,直到相邻两次迭代结果的差值小于预设的精度阈值。
Q2: 根号符号在复数范围内有何特殊含义?
A2: 在复数范围内,根号符号被赋予了更广泛的含义,对于任意复数z = a + bi(其中a和b为实数),我们可以定义其n次方根(n为正整数),特别地,当n=2时,我们得到复数z的平方根,与实数范围内的平方根不同,复数的平方根并不唯一,每个非零复数都有两个不同的平方根(考虑重根情况),这些平方根可以通过复数的指数和对数形式来表示和计算。
各位小伙伴们,我刚刚为大家分享了有关“根号符号”的知识,希望对你们有所帮助。如果您还有其他相关问题需要解决,欢迎随时提出哦!
本站发布或转载的文章及图片均来自网络,其原创性以及文中表达的观点和判断不代表本站,有问题联系侵删!
本文链接:https://www.xixizhuji.com/fuzhu/4374.html