如何利用C语言实现高效的网络流算法？

网络流是网络最优化问题的重要部分，应用广泛。随着技术发展，形成了完善的理论体系和有效算法，包括最大流、最小费用流等。

一、基本概念

1、流网络：是一个有向图(G=(V,E))，包含点集(V)和边集(E)，其中有一个源点(s)和一个汇点(t)，对于每条边((u,v)in E)，都有一个容量(c(u,v))，表示该边单位时间可以流过的最大水量。

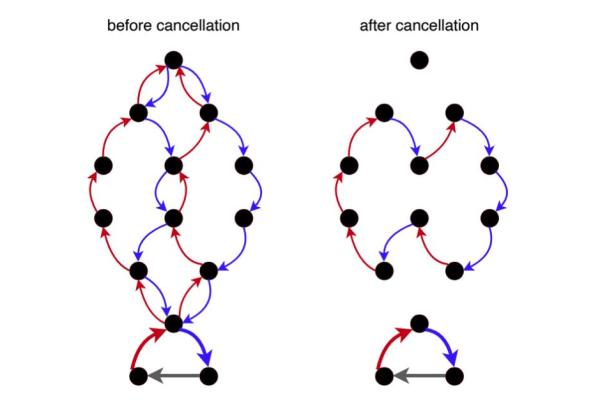
2、可行流：记为(f(u,v))，表示边(e:urightarrow v)当前的流量，需要满足两个约束条件，一是容量限制，即(0leq f(u,v)leq c(u,v))；二是流量守恒，即除了源点、汇点外，其他点流入的流量等于流出的流量，用公式表示为(sum_{(u,x)in E}f(u,x)=sum_{(x,v)in E}f(x,v))。

3、最大流：在(G)中可行流构成的集合中，流量值最大的元素，通常用单位时间流出源点的流量来刻画，记为(|f|=sum_{(s,x)in E}f(s,x)-sum_{(y,s)in E}f(y,s))。

4、残留网络：总是针对原图(G=(V,E))中的某一个可行流而言，记为(G_f=(V_f,E_f))。(V_f=V)，(E_f = Ecup E’)，(E’)是(E)中所有的反向边，残留网络中的容量记为(c'(u,v))，定义为(left{begin{matrix}c(u,v)-f(u,v),&(u,v)in E\f(v,u),&(v,u)in Eend{matrix}right.)。

5、增广路径：如果从源点(s)出发沿着残留网络中容量大于(0)的边可以走到汇点(t)，那么将走过的边所组成的路径称为增广路径。

6、割：是网络中顶点的一个划分，把顶点划分为两个顶点集合(S)和(T)，其中源点(sin S)，汇点(tin T)，且(Scup T = V)，(Scap T=emptyset)。

7、最小割：是(G)中所有割组成的集合中容量最小的元素，记为([S,T])，其容量为(c(S,T)=sum_{uin S}sum_{vin T}c(u,v))。

8、最大流最小割定理：(f)是最大流当且仅当不存在增广路，即(G_f)中不存在增广路，任意割的容量(leq)任意可行流的流量，即对于任意一个可行流(f)和任意一个割((S,T))，有(f(S,T)leq c(S,T))，当达到最大流时，(G_f)中不存在增广路，(f(S,T)=c(S,T))。

二、算法介绍

1、EK算法：是一种单路增广算法，基于广度优先搜索（BFS）来寻找增广路，每次找到增广路后，根据该增广路中所有边的最小容量来增加流量，然后更新残留网络，重复这个过程直到找不到增广路为止。

2、Dinic算法：是一种多路增广算法，通过分层图的思想来同时找出多条增广路，从而提高增广的效率，它首先构建分层图，然后在每层中进行BFS寻找增广路，最后根据找到的增广路来更新流量和残留网络。

3、ISAP算法：是一种改进的Dinic算法，它在寻找增广路时使用了更高效的数据结构，如动态树等，以提高算法的执行效率，ISAP算法在一些复杂的网络流问题中表现较好。

三、应用案例

1、运输问题：假设有多个仓库和多个销售点，每个仓库到每个销售点之间都有一定的运输成本和运输能力限制，现在要确定从各个仓库运往各个销售点的货物数量，使得总运输成本最低且满足各销售点的需求，可以将仓库看作源点，销售点看作汇点，运输能力和成本看作边的容量和权重，通过求解最大流或最小费用最大流问题来确定最优的运输方案。

2、工程进度安排：在一个工程项目中，有多个任务需要依次完成，每个任务都有其持续时间和资源需求，同时任务之间存在先后顺序的约束，可以将任务看作节点，任务之间的依赖关系看作有向边，资源的可用量看作边的容量，通过求解网络流问题来确定每个任务的最早开始时间和最晚结束时间，从而合理安排工程进度。

3、图像分割：在图像处理中，可以将图像中的像素点看作节点，像素之间的相似性或连通性看作边的容量，通过求解网络流问题来实现对图像的分割，例如将图像分割成不同的区域，以便进行进一步的分析和处理。

四、FAQs

1、网络流问题一定是从单个源点到单个汇点吗？：不一定，虽然很多经典的网络流问题都是从单个源点到单个汇点的模式，但在实际应用中，也存在多个源点和多个汇点的情况，此时可以将多个源点合并为一个虚拟源点，将多个汇点合并为一个虚拟汇点，然后在这个扩展的网络中求解网络流问题。

2、如何判断一个网络流是否达到了最大流？：可以通过检查残留网络中是否存在增广路来判断，如果在残留网络中找不到从源点到汇点的增广路，那么当前流就是最大流。

3、网络流算法的时间复杂度是多少？：不同的网络流算法时间复杂度不同，EK算法的时间复杂度为(O(VE^2))，Dinic算法的时间复杂度为(O(V^2E))，ISAP算法的时间复杂度为(O(VElog V))。