当前位置：首页 > 行业动态 > 正文

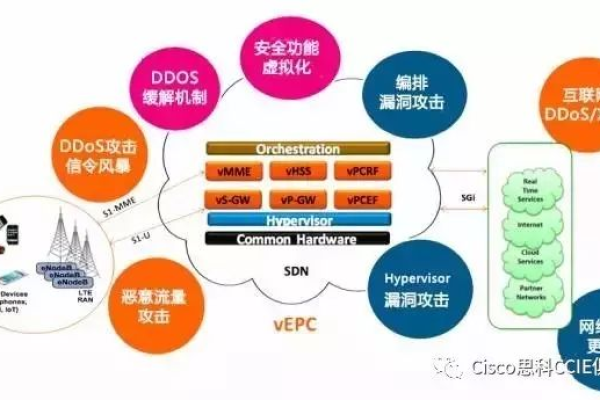
如何有效利用存储结构优化数据管理？

admin
行业动态
2025-01-24
2256

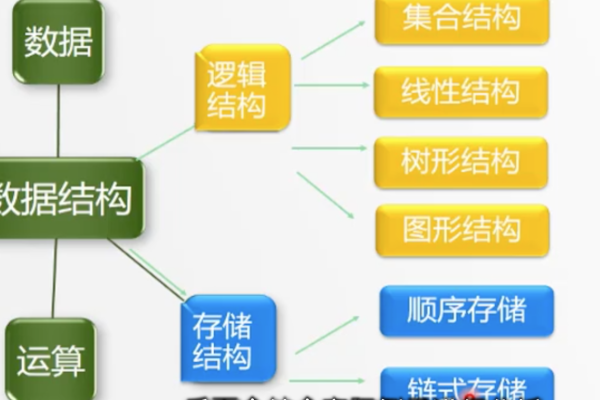
存储结构是数据元素及其逻辑关系在计算机中的表示，主要有顺序、链式、索引和哈希存储结构，其选择取决于具体需求和场景。

存储结构是计算机科学中的一个核心概念，它决定了数据在计算机内存中的组织、管理和存储方式，不同的存储结构适用于不同的应用场景，选择合适的存储结构可以显著提高程序的性能和效率，以下是几种常见的存储结构及其使用方法的详细解析：

如何有效利用存储结构优化数据管理？第1张

数组（Array）

定义与特点：

数组是一种线性存储结构，它将相同类型的元素按顺序存储在连续的内存空间中。

访问速度快，可以通过索引直接访问任意元素。

数组大小固定，插入和删除操作相对复杂。

使用场景：

需要快速随机访问元素的场景，如图像处理中的像素点阵。

数据量不大且预先知道的情况下，如小型数据集的排序。

示例代码（Python）：

创建一个整数数组
arr = [1, 2, 3, 4, 5]
访问第一个元素
print(arr[0])  # 输出: 1
修改第三个元素
arr[2] = 10
print(arr)  # 输出: [1, 2, 10, 4, 5]

链表（Linked List）

定义与特点：

链表是一种非线性存储结构，由一系列节点组成，每个节点包含数据部分和指向下一个节点的指针。

动态大小，插入和删除操作灵活。

访问速度慢，需从头开始遍历。

使用场景：

数据量较大且频繁进行插入和删除操作的场景，如实现多项式的加减运算。

需要动态调整大小的数据结构，如队列和栈的实现。

示例代码（Python，使用内置deque模拟链表操作）：

from collections import deque
创建一个双向链表
linked_list = deque([1, 2, 3])
在链表头部添加元素
linked_list.appendleft(0)
print(linked_list)  # 输出: deque([0, 1, 2, 3])
删除链表尾部元素
linked_list.pop()
print(linked_list)  # 输出: deque([0, 1, 2])

栈（Stack）

定义与特点：

栈是一种后进先出（LIFO）的线性存储结构，只允许在一端进行插入和删除操作。

常用于表达式求值、函数调用栈等。

使用场景：

需要逆序处理数据的场景，如浏览器的历史记录功能。

实现递归算法时，用于保存中间状态。

示例代码（Python）：

stack = []
入栈操作
stack.append(1)
stack.append(2)
stack.append(3)
print(stack)  # 输出: [1, 2, 3]
出栈操作
top_element = stack.pop()
print(top_element)  # 输出: 3
print(stack)        # 输出: [1, 2]

队列（Queue）

定义与特点：

队列是一种先进先出（FIFO）的线性存储结构，只允许在一端插入元素，在另一端删除元素。

常用于任务调度、广度优先搜索等。

使用场景：

需要顺序处理数据的场景，如打印任务队列。

实现多线程或多进程间的同步与通信。

示例代码（Python）：

from queue import Queue
queue = Queue()
入队操作
queue.put(1)
queue.put(2)
queue.put(3)
print(queue.queue)  # 输出: deque([1, 2, 3])
出队操作
first_element = queue.get()
print(first_element)  # 输出: 1
print(queue.queue)    # 输出: deque([2, 3])

5. 树（Tree）与二叉树（Binary Tree）

定义与特点：

树是一种分层结构，每个节点可以有多个子节点，但只有一个父节点。

二叉树是一种特殊的树，每个节点最多有两个子节点。

适用于表示层次关系、实现搜索算法等。

使用场景：

文件系统的目录结构。

实现高效的搜索和排序算法，如二叉搜索树、平衡二叉树等。

示例代码（Python，简单二叉树实现）：

class TreeNode:
    def __init__(self, value=0, left=None, right=None):
        self.value = value
        self.left = left
        self.right = right
创建一个简单的二叉树
root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.left = TreeNode(4)
root.left.right = TreeNode(5)
前序遍历二叉树
def preorder_traversal(node):
    if node:
        print(node.value, end=' ')
        preorder_traversal(node.left)
        preorder_traversal(node.right)
preorder_traversal(root)  # 输出: 1 2 4 5 3

图（Graph）

定义与特点：

图是由节点（顶点）和连接这些节点的边组成的结构，可以是有向图或无向图。

用于表示复杂的网络关系，如社交网络、交通网络等。

存储方式多样，包括邻接矩阵、邻接表等。

使用场景：

路径规划、推荐系统、网络流分析等。

任何需要表示实体间复杂关系的场景。

示例代码（Python，使用邻接表表示图）：

graph = {
    'A': ['B', 'C'],
    'B': ['A', 'D', 'E'],
    'C': ['A', 'F'],
    'D': ['B'],
    'E': ['B', 'F'],
    'F': ['C', 'E']
}
深度优先搜索（DFS）遍历图
def dfs(graph, start, visited=None):
    if visited is None:
        visited = set()
    visited.add(start)
    print(start, end=' ')
    for neighbor in graph[start]:
        if neighbor not in visited:
            dfs(graph, neighbor, visited)
dfs(graph, 'A')  # 输出: A B D E F C