如何用Java实现Dijkstra算法？

Dijkstra 算法是一种用于计算单源最短路径的贪心算法。在 Java 中，可以使用优先队列实现 Dijkstra 算法。

Dijkstra算法是一种经典的单源最短路径算法，用于计算图中一个节点到其他所有节点的最短路径，该算法由荷兰计算机科学家艾兹格·戴克斯特拉于1956年提出，适用于边权重均为非负的图，以下是对Dijkstra算法的详细解释及其在Java中的实现。

Dijkstra算法的基本思想

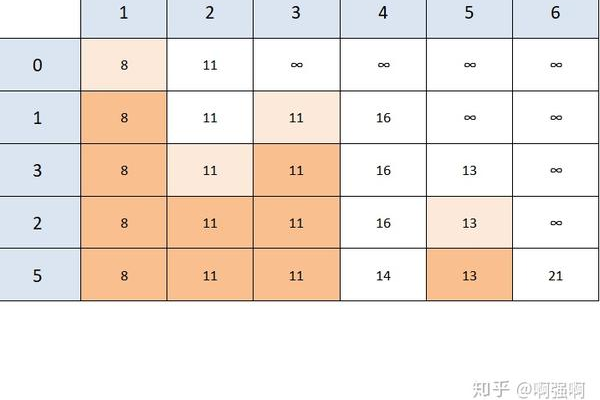
Dijkstra算法的核心思想是贪心策略，它从起点开始，逐步扩展最短路径树，直至包含所有节点，具体步骤如下：

1、初始化：将起点到其他所有节点的距离设为无穷大，起点到自身的距离设为0，创建一个集合S，用于存放已访问的节点，初始时只包含起点。

2、选择节点：在未访问的节点中选择距离起点最近的节点u，将其加入集合S。

3、更新距离：对于节点u的每一个邻居节点v，如果通过节点u到达节点v的距离比已知的距离更短，则更新节点v的距离值。

4、重复：重复步骤2和3，直到所有节点都被访问。

Java实现Dijkstra算法

以下是使用Java实现Dijkstra算法的示例代码：

import java.util.Arrays;
import java.util.PriorityQueue;
public class DijkstraAlgorithm {
    public static void calculateShortestPath(int[][] graph, int source) {
        int vertices = graph.length;
        int[] distances = new int[vertices];
        boolean[] visited = new boolean[vertices];
        Arrays.fill(distances, Integer.MAX_VALUE);
        distances[source] = 0;
        PriorityQueue<Integer> queue = new PriorityQueue<>(vertices, (a, b) -> distances[a] distances[b]);
        queue.add(source);
        while (!queue.isEmpty()) {
            int current = queue.poll(); // 取出当前最小距离的顶点
            if (visited[current]) continue;
            visited[current] = true;
            for (int i = 0; i < vertices; i++) {
                if (graph[current][i] > 0 && !visited[i]) {
                    int distanceThroughCurrent = distances[current] + graph[current][i];
                    if (distanceThroughCurrent < distances[i]) {
                        distances[i] = distanceThroughCurrent;
                        queue.add(i);
                    }
                }
            }
        }
        System.out.println("Vertex Distance from Source");
        for (int i = 0; i < vertices; i++) {
            System.out.println(i + "tt" + distances[i]);
        }
    }
    public static void main(String[] args) {
        int[][] graph = {
                {0, 2, 4, 0, 0, 0},
                {2, 0, 3, 5, 0, 0},
                {4, 3, 0, 1, 7, 0},
                {0, 5, 1, 0, 4, 2},
                {0, 0, 7, 4, 0, 6},
                {0, 0, 0, 2, 6, 0}
        };
        int sourceVertex = 0;
        calculateShortestPath(graph, sourceVertex);
    }
}

代码说明

1、初始化：distances数组用于存储起点到各个顶点的最短距离，初始时除了起点自身为0外，其余都为无穷大（Integer.MAX_VALUE）。visited数组用于标记是否已经访问过某个顶点。

2、优先队列：使用优先队列来存储和选择当前距离最小的节点，优先队列根据distances数组的值进行排序。

3、主循环：不断从优先队列中取出当前距离最小的节点，更新其邻接节点的距离，并将更新后的邻接节点加入优先队列。

4、输出结果：遍历完成后，输出起点到各个顶点的最短距离。

相关问答FAQs

Q1: Dijkstra算法的时间复杂度是多少？

A1: Dijkstra算法的时间复杂度主要取决于优先队列的操作，使用二叉堆实现优先队列时，时间复杂度为O((V + E) log V)，其中V是顶点数，E是边数，使用斐波那契堆时，时间复杂度可以降低到O(E + V log V)。

Q2: Dijkstra算法适用于哪些类型的图？

A2: Dijkstra算法适用于边权重均为非负的图，如果图中存在负权边，Dijkstra算法可能无法正确计算出最短路径。

小编有话说

Dijkstra算法作为经典的最短路径算法，广泛应用于路由选择、网络调度等领域，虽然其时间复杂度较高，但通过优化数据结构和算法细节，可以在一定程度上提高性能，掌握Dijkstra算法不仅有助于理解图论中的最短路径问题，还能在实际编程中解决许多相关问题，希望本文能帮助读者更好地理解和实现Dijkstra算法。