bp神经网络程序代码

BP神经网络程序代码实现指南

BP神经网络(Back Propagation Neural Network)是最常见的人工神经网络之一，广泛应用于模式识别、函数逼近、数据分类等领域，下面我们将详细介绍BP神经网络的实现代码及其原理。

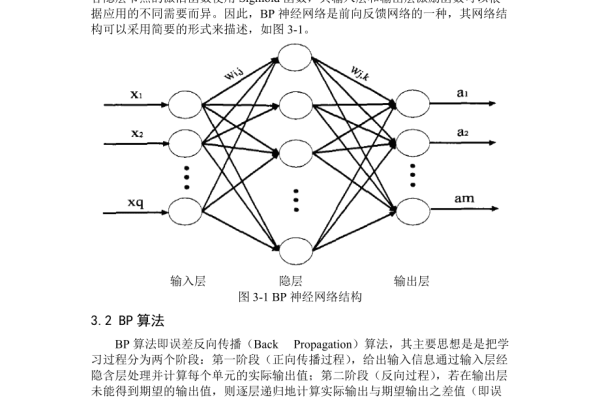
Python实现BP神经网络

import numpy as np
import matplotlib.pyplot as plt
class BPNeuralNetwork:
    def __init__(self, input_size, hidden_size, output_size):
        # 初始化权重和偏置
        self.W1 = np.random.randn(input_size, hidden_size) * 0.01
        self.b1 = np.zeros((1, hidden_size))
        self.W2 = np.random.randn(hidden_size, output_size) * 0.01
        self.b2 = np.zeros((1, output_size))
    def sigmoid(self, x):
        return 1 / (1 + np.exp(-x))
    def sigmoid_derivative(self, x):
        return x * (1 - x)
    def forward(self, X):
        # 前向传播
        self.z1 = np.dot(X, self.W1) + self.b1
        self.a1 = self.sigmoid(self.z1)
        self.z2 = np.dot(self.a1, self.W2) + self.b2
        self.a2 = self.sigmoid(self.z2)
        return self.a2
    def backward(self, X, y, output, learning_rate):
        # 反向传播
        error = y - output
        d_output = error * self.sigmoid_derivative(output)
        error_hidden = d_output.dot(self.W2.T)
        d_hidden = error_hidden * self.sigmoid_derivative(self.a1)
        # 更新权重和偏置
        self.W2 += self.a1.T.dot(d_output) * learning_rate
        self.b2 += np.sum(d_output, axis=0, keepdims=True) * learning_rate
        self.W1 += X.T.dot(d_hidden) * learning_rate
        self.b1 += np.sum(d_hidden, axis=0, keepdims=True) * learning_rate
    def train(self, X, y, epochs=10000, learning_rate=0.1):
        loss_history = []
        for i in range(epochs):
            output = self.forward(X)
            self.backward(X, y, output, learning_rate)
            # 计算损失
            loss = np.mean(np.square(y - output))
            loss_history.append(loss)
            if i % 1000 == 0:
                print(f"Epoch {i}, Loss: {loss}")
        plt.plot(loss_history)
        plt.title('Training Loss')
        plt.xlabel('Epoch')
        plt.ylabel('Loss')
        plt.show()
    def predict(self, X):
        return self.forward(X)

MATLAB实现BP神经网络

classdef BPNeuralNetwork
    properties
        W1
        b1
        W2
        b2
    end
    methods
        function obj = BPNeuralNetwork(input_size, hidden_size, output_size)
            % 初始化权重和偏置
            obj.W1 = randn(input_size, hidden_size) * 0.01;
            obj.b1 = zeros(1, hidden_size);
            obj.W2 = randn(hidden_size, output_size) * 0.01;
            obj.b2 = zeros(1, output_size);
        end
        function y = sigmoid(~, x)
            y = 1 ./ (1 + exp(-x));
        end
        function y = sigmoid_derivative(~, x)
            y = x .* (1 - x);
        end
        function output = forward(obj, X)
            % 前向传播
            obj.z1 = X * obj.W1 + obj.b1;
            obj.a1 = obj.sigmoid(obj.z1);
            obj.z2 = obj.a1 * obj.W2 + obj.b2;
            output = obj.sigmoid(obj.z2);
        end
        function backward(obj, X, y, output, learning_rate)
            % 反向传播
            error = y - output;
            d_output = error .* obj.sigmoid_derivative(output);
            error_hidden = d_output * obj.W2';
            d_hidden = error_hidden .* obj.sigmoid_derivative(obj.a1);
            % 更新权重和偏置
            obj.W2 = obj.W2 + obj.a1' * d_output * learning_rate;
            obj.b2 = obj.b2 + sum(d_output, 1) * learning_rate;
            obj.W1 = obj.W1 + X' * d_hidden * learning_rate;
            obj.b1 = obj.b1 + sum(d_hidden, 1) * learning_rate;
        end
        function train(obj, X, y, epochs, learning_rate)
            loss_history = zeros(1, epochs);
            for i = 1:epochs
                output = obj.forward(X);
                obj.backward(X, y, output, learning_rate);
                % 计算损失
                loss = mean((y - output).^2);
                loss_history(i) = loss;
                if mod(i, 1000) == 0
                    fprintf('Epoch %d, Loss: %fn', i, loss);
                end
            end
            figure;
            plot(loss_history);
            title('Training Loss');
            xlabel('Epoch');
            ylabel('Loss');
        end
        function output = predict(obj, X)
            output = obj.forward(X);
        end
    end
end

神经网络参数调优建议

1. 学习率选择：通常设置在0.01到0.1之间，过大可能导致震荡，过小则收敛慢
2. 隐藏层节点数：一般取输入节点数的1/2到2/3，可通过交叉验证确定最佳值
3. 激活函数：除了sigmoid，还可以尝试ReLU、tanh等函数
4. 正则化：添加L1/L2正则化防止过拟合
5. 批量训练：将数据分成小批量进行训练，提高效率

应用案例

# 示例：使用BP神经网络解决XOR问题
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
y = np.array([[0], [1], [1], [0]])
# 创建神经网络
nn = BPNeuralNetwork(input_size=2, hidden_size=4, output_size=1)
# 训练网络
nn.train(X, y, epochs=10000, learning_rate=0.1)
# 预测结果
print("Predictions:")
for i in range(len(X)):
    print(f"Input: {X[i]}, Predicted: {nn.predict(X[i].reshape(1, -1))[0][0]:.4f}")

常见问题解答

Q: BP神经网络为什么会出现梯度消失问题？
A: 当使用sigmoid或tanh激活函数时，在反向传播过程中梯度会随着层数的增加而指数级减小，导致深层网络难以训练。

Q: 如何改进BP神经网络的训练效果？
A: 可以尝试使用ReLU激活函数、批标准化、调整学习率衰减策略、使用Adam等优化算法。

Q: BP神经网络适合处理什么类型的数据？
A: BP神经网络适合处理中小规模的结构化数据，在图像、语音等非结构化数据上效果不如卷积神经网络和循环神经网络。

参考文献

1. Rumelhart, D. E., Hinton, G. E., & Williams, R. J. (1986). Learning representations by back-propagating errors. Nature, 323(6088), 533-536.
2. Haykin, S. (2009). Neural networks and learning machines (Vol. 3). Pearson Upper Saddle River, NJ, USA:.
3. 周志华. (2016). 机器学习. 清华大学出版社.