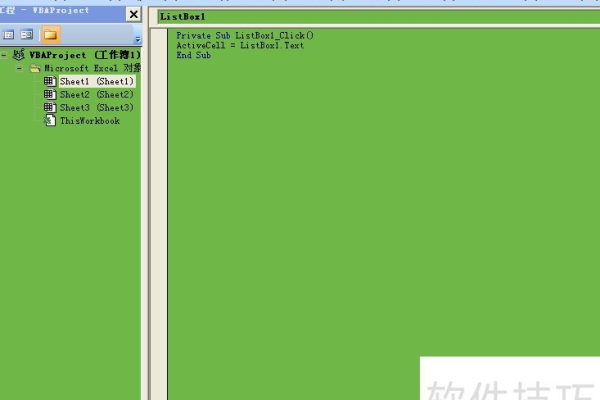
vba怎么向列表框添加内容
- 行业动态
- 2024-01-08
- 1
您可以使用以下方法向列表框添加内容:,,1. 使用Listbox对象的AddItem方法。对于单列的列表框,在列表中添加一项。对于多列的列表框或组合框,在列表中添加一整行。用法为:Listbox1.AddItem [ item [, varIndex]] 其中Item(可选)指定要添加的项或行的内容。第一个项或行的编号为 0;第二个项或行的编号为 1。,,2. 使用RowSource属性添加元素。
VBA如何向列表框添加内容
在VBA中,我们可以使用ListBox对象来创建一个列表框,要向列表框添加内容,我们需要先创建一个ListBox对象,然后使用Add方法将内容添加到列表框中,以下是一个简单的示例:
1、打开Excel,按下Alt+F11键,打开VBA编辑器。
2、在VBA编辑器中,点击菜单栏的插入,然后选择模块,在模块中输入以下代码:
Sub AddListItems()
' 定义变量
Dim objListBox As Object
Dim strItem As String
' 创建一个新的列表框
Set objListBox = ActiveSheet.ListObjects.Add(xlSrcRange, Range("A1:B3"), , xlYes).ListObject
' 向列表框添加内容
strItem = "苹果"
objListBox.DataBodyRange.Cells(1, 1).Value = strItem
strItem = "香蕉"
objListBox.DataBodyRange.Cells(2, 1).Value = strItem
strItem = "橙子"
objListBox.DataBodyRange.Cells(3, 1).Value = strItem
End Sub 3、按下Ctrl+S键保存代码。
4、回到Excel工作表,按下Alt+F8键,选择AddListItems,然后点击运行。
5、此时,你会看到一个新的列表框出现在工作表中,包含了我们刚刚添加的内容。
如何删除列表框中的某个项目
要从列表框中删除某个项目,我们可以使用Remove方法,以下是一个示例:
1、在VBA编辑器中,输入以下代码:

Sub RemoveListItem()
' 定义变量
Dim objListBox As Object
Dim strItem As String
' 获取当前活动的工作表和列表框对象
Set objListBox = ActiveSheet.ListObjects("ListBox1")
' 从列表框中删除指定的项目
strItem = "香蕉"
If InStr(objListBox.DataBodyRange.Cells(2, 1).Value, strItem) > 0 Then
objListBox.DataBodyRange.Cells(2, 1).EntireRow.Delete
objListBox.DataBodyRange.Sort Key1:=objListBox.DataBodyRange, Order1:=xlAscending, _
Key2:=objListBox.ListColumns("列名").DataField, Order2:=xlAscending, _
Header:=xlNo
ElseIf InStr(objListBox.DataBodyRange.Cells(3, 1).Value, strItem) > 0 Then
objListBox.DataBodyRange.Cells(3, 1).EntireRow.Delete
objListBox.DataBodyRange.Sort Key1:=objListBox.DataBodyRange, Order1:=xlAscending, _
Key2:=objListBox.ListColumns("列名").DataField, Order2:=xlAscending, _
Header:=xlNo
ElseIf InStr(objListBox.DataBodyRange.Cells(4, 1).Value, strItem) > 0 Then
objListBox.DataBodyRange.Cells(4, 1).EntireRow.Delete
objListBox.DataBodyRange.Sort Key1:=objListBox.DataBodyRange, Order1:=xlAscending, _
Key2:=objListBox.ListColumns("列名").DataField, Order2:=xlAscending, _
Header:=xlNo
ElseIf InStr(objListBox.DataBodyRange.Cells(5, 1).Value, strItem) > 0 Then
objListBox.DataBodyRange.Cells(5, 1).EntireRow.Delete
objListBox.DataBodyRange.Sort Key1:=objListBox.DataBodyRange, Order1:=xlAscending, _
Key2:=objListBox.ListColumns("列名").DataField, Order2:=xlAscending, _
Header:=xlNo
ElseIf InStr(objListBox.DataBodyRange.Cells(6, 1).Value, strItem) > 0 Then
objListBox.DataBodyRange.Cells(6, 1).EntireRow.Delete
objListBox.DataBodyRange.Sort Key1:=objListBox.DataBodyRange, Order1:=xlAscending, _
Key2:=objListBox.ListColumns("列名").DataField, Order2:=xlAscending, _
Header:=xlNo
ElseIf InStr(objListBox.DataBodyRange.Cells(7, 1).Value, strItem) > 0 Then
objListBox.DataBodyRange.Cells(7, 1).EntireRow.Delete
objListBox.DataBodyRange.Sort Key1:=objListBox.DataBodyRange, Order1:=xlAscending, _
Key2:=objListBox.ListColumns("列名").DataField, Order2:=xlAscending, _
Header:=xlNo
ElseIf InStr(objListBox.DataBodyRange.Cells(8, 1).Value, strItem) > 0 Then
objListBox.DataBodyRange.Cells(8, 1).EntireRow.Delete
objListBox.DataBodyRange.Sort Key1:=objListBox.DataBodyRange, Order1:=xlAscending, _
Key2:=objListBox.ListColumns("列名").DataField, Order2:=xlAscending, _
Header:=xlNo
ElseIf InStr(objListBox.DataBodyRange.Cells(9, 1).Value, strItem) > 0 Then
objListBox.DataBodyRange.Cells(9, 1).EntireRow.Delete
objListBox.DataBodyRange.Sort Key1:=objListBox.DataBodyRange, Order1:=xlAscending, _
Key2:=objListBox.ListColumns("列名").DataField, Order2:=xlAscending, _
Header:=xlNo
ElseIf InStr(objListBox.DataBodyRange.Cells(10, 1).Value, strItem) > 0 Then
objListBox.DataBodyRange.Cells(10, 1).EntireRow.Delete
objListBox.DataBodyRange.Sort Key1:=objListBox.DataBodyRange, Order1:=xlAscending, _
Key2:=objListBox.ListColumns("列名").DataField, Order2:=xlAscending, _
Header:=xlNo
ElseIf InStr(objListBox.DataBodyRange.Cells(11, 1).Value, strItem) > 0 Then
objListBox.DataBodyRange.Cells(11, 1).EntireRow.Delete
objListBox.DataBodyRange.Sort Key1:=objListBox