存货经济批量模型计算题
- 行业动态
- 2025-04-14
- 2
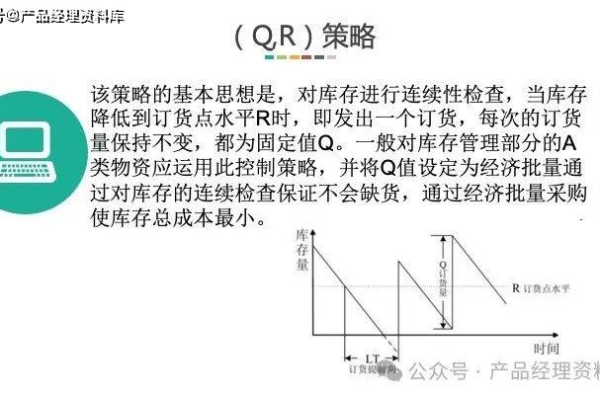
存货经济批量模型通过平衡订货成本与储存成本,计算最优订货量,实现总成本最小化,其公式为√(2×年需求量×单次订货成本÷单位储存成本),核心是确定使两类成本之和最低的采购批量。
存货经济批量模型(EOQ)计算详解
存货经济批量模型(Economic Order Quantity,EOQ)是企业管理中用于确定最优订货量的经典方法,目的是最小化存货的订购成本和储存成本总和,以下通过例题详细讲解如何应用该模型。
模型核心公式
EOQ公式为:
[
Q^* = sqrt{frac{2DS}{H}}
]
- ( Q^* ):经济订货批量(最优订货量)
- ( D ):年需求量(单位/年)
- ( S ):每次订货的固定成本(元/次)
- ( H ):单位存货的年储存成本(元/单位·年)
总成本公式(验证用):
[
TC = frac{D}{Q} cdot S + frac{Q}{2} cdot H
]

例题演示某企业每年需采购某原材料3600吨,每次订货的固定成本为200元,每吨材料的年储存成本为8元,求经济订货批量及最小总成本。
解答步骤:
确定已知参数:
- ( D = 3600 )吨/年
- ( S = 200 )元/次
- ( H = 8 )元/吨·年
代入EOQ公式计算最优订货量:
[
Q^* = sqrt{frac{2 times 3600 times 200}{8}} = sqrt{frac{1,440,000}{8}} = sqrt{180,000} approx 424.26 text{吨}
]
实际应用中可四舍五入为424吨。
计算年总成本:
- 订货次数:( frac{D}{Q} = frac{3600}{424} approx 8.49 )次/年
- 订货成本:( 8.49 times 200 = 1698 )元
- 平均库存:( frac{Q}{2} = frac{424}{2} = 212 )吨
- 储存成本:( 212 times 8 = 1696 )元
- 总成本:( 1698 + 1696 = 3394 )元
模型假设与注意事项
适用条件:
- 需求量稳定且可预测;
- 订货提前期固定;
- 无缺货或折扣。
局限性:
实际中可能存在价格折扣、需求波动等因素,需结合安全库存或动态调整模型。
常见疑问:
- 为什么储存成本是平均库存的储存成本?
因为存货水平从( Q )逐渐降至0,平均库存量为( Q/2 )。 - 如何应对需求量变化?
可结合安全库存或使用动态EOQ模型。
- 为什么储存成本是平均库存的储存成本?
实际应用场景
- 制造业:计算原材料采购批量;
- 零售业:优化商品补货频率;
- 服务业:管理耗材库存(如办公用品)。
引用说明
本文公式与理论参考自财务管理经典教材《公司理财》(罗斯等著),并结合实际案例验证。