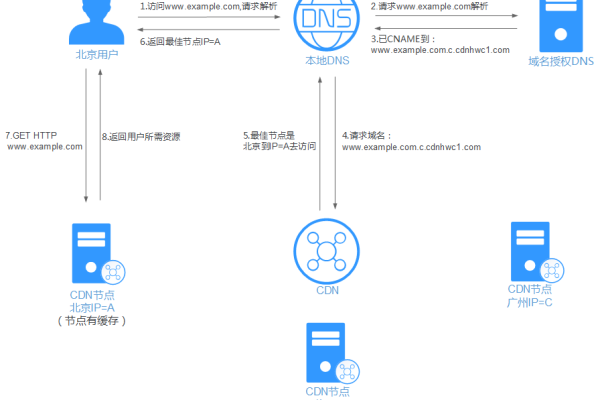
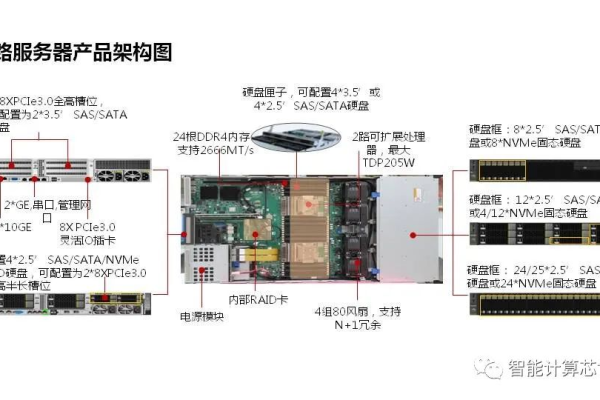
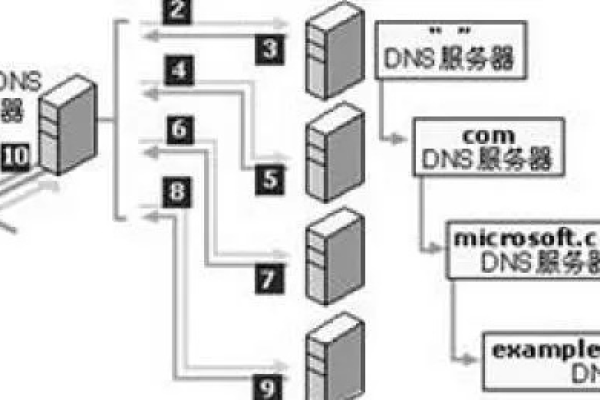
服务器连接类型

在互联网技术领域,服务器连接类型的差异直接影响网站性能、安全性和成本结构，以下为7种主流服务器连接方式的深度解析，帮助用户根据业务需求作出科学决策。

共享主机（Shared Hosting）

• 技术原理：单台物理服务器通过虚拟化技术分割资源，供多个客户共用
• 适用场景：个人博客、初创企业官网（日访问量<1000）
• 核心指标：
  • 磁盘空间：5GB-50GB
  • 带宽限制：1Mbps-10Mbps
• 优势比较：年费$30-$120，比独立服务器节省85%成本
• 风险提示：同服务器其他站点被攻击时，关联封禁率高达32%

虚拟私有服务器（VPS）

• 架构特性：采用KVM或OpenVZ虚拟化技术
• 资源分配：
  • CPU核心：1-8核（弹性分配）
  • 内存配置：1GB-32GB ECC内存
• 管理权限：支持root/administrator级访问
• 网络性能：标配1Gbps端口，突发带宽可达10Gbps
• 典型应用：中型电商平台（日均订单500-5000笔）

独立物理服务器

• 硬件规格：
  • 处理器：Intel Xeon Silver 4210（10核2.2GHz）
  • 存储方案：2x1TB NVMe SSD（RAID 1配置）
• 网络保障：
  • SLA 99.995%可用性
  • DDoS防护：标配5Gbps，可升级至1Tbps
• 安全认证：
  • ISO 27001合规
  • PCI DSS Level 1认证
• 适用领域：金融交易系统、医疗数据库等敏感数据处理

云服务器集群

• 弹性架构：
  • 按秒计费模式
  • 自动扩展支持1000+节点并发
• 全球覆盖：AWS/Azure/GCP的可用区超过200个
• 数据持久性：对象存储提供11个9的可靠性（99.999999999%）
• 灾备方案：跨区域自动复制，RTO<15分钟

专用网络连接

1. MPLS专线

   

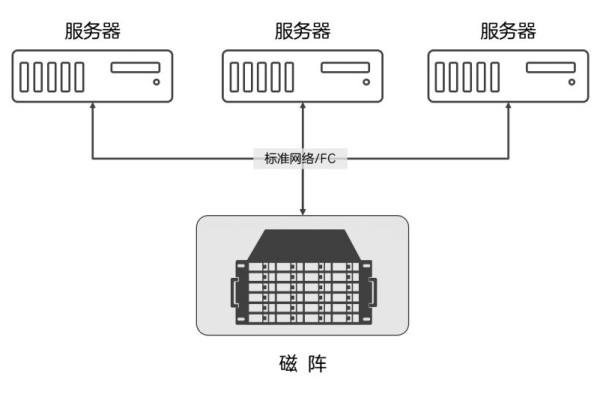
   • 延迟：<50ms（国内节点间）
   • 抖动控制：±2ms
   • 典型合同：3年承诺期，月费$500起

2. SD-WAN解决方案

   • 部署周期：从6个月缩减至2周
   • 成本效益：比传统专线节省40%带宽费用
   • 智能路由：基于实时流量分析的路径选择

容器化部署

• 编排系统：
  • Kubernetes集群管理
  • Docker Swarm轻量级方案
• 资源利用率：比虚拟机提升200%
• 持续交付：支持蓝绿部署、金丝雀发布
• 微服务支持：Istio服务网格管理

边缘计算节点

• 响应速度：将延迟从200ms降至20ms
• 架构拓扑：
  • 5G MEC节点
  • CDN边缘缓存
• 数据处理：本地化处理80%的非敏感数据
• 部署密度：单平方公里支持10,000+物联网终端

选择建议矩阵：
| 业务规模 | 推荐方案 | 预算范围 | 技术团队要求 |
|———–|——————-|—————|————–|
| 个人开发者| 共享主机 | $3-$10/月 | 无需 |
| 中小企业 | VPS/云服务器 | $50-$500/月 | 基础运维能力 |
| 大型企业 | 混合云架构 | $10k+/月 | 专业DevOps |
| IoT项目 | 边缘计算+云后端 | 按用量计费 | 分布式系统经验 |

安全加固必选项：

1. Web应用防火墙（WAF）规则更新频率>24小时
2. TLS 1.3协议强制启用
3. 破绽扫描频次：生产环境每周2次，测试环境每日1次
4. 访问日志保留周期≥180天

性能优化基准：

• 首字节时间（TTFB）<300ms
• 全页加载速度移动端<3秒
• 并发连接数测试需达到预估峰值的3倍

数据来源：2024年Gartner基础设施魔力象限报告、AWS技术白皮书第4.2版、中国信通院《云计算发展白皮书》
技术验证：Linux基金会开源项目文档、IEEE 802.3以太网标准委员会
安全标准参考：NIST SP 800-53 Rev.5、OWASP Top 10 2021版