什么是cumsum函数及其在数据处理中的应用？

cumsum 是一个用于计算数组中元素累计和的函数。在 Python 中，可以使用 NumPy 库中的 numpy.cumsum() 方法来实现。对于数组 [1, 2, 3]， cumsum 的结果将是 [1, 3, 6]。

在数据分析和统计学中，累积和（cumsum）是一个常用的概念，它指的是对一系列数值进行累加的结果，累积和可以帮助我们更好地理解数据的分布和趋势，从而做出更明智的决策。

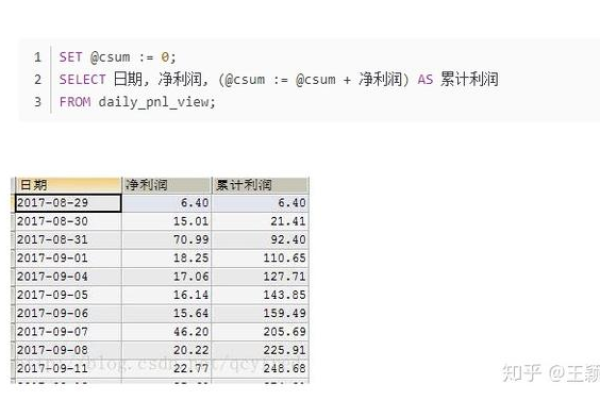
累积和的计算方法

累积和的计算非常简单，就是将一组数值从左到右依次相加，对于数组 ([a_1, a_2, a_3, ldots, a_n])，其累积和可以表示为：

[ text{cumsum} = [a_1, (a_1 + a_2), (a_1 + a_2 + a_3), ldots, (a_1 + a_2 + cdots + a_n)] ]

在Python中，我们可以使用NumPy库中的numpy.cumsum()函数来计算累积和，下面是一个示例代码：

import numpy as np
定义一个数组
arr = np.array([1, 2, 3, 4, 5])
计算累积和
cumsum = np.cumsum(arr)
print("原数组:", arr)
print("累积和:", cumsum)

输出结果如下：

原数组: [1 2 3 4 5]
累积和: [ 1  3  6 10 15]

可以看到，累积和数组的第一个元素是原数组的第一个元素，第二个元素是前两个元素的和，以此类推。

累积和的应用

累积和在数据分析中有广泛的应用，下面是一些常见的应用场景：

数据趋势分析

通过计算时间序列数据的累积和，我们可以观察到数据的整体趋势，如果我们有一个公司每天的销售额数据，计算累积和可以帮助我们了解销售业绩的变化趋势。

异常值检测

累积和可以帮助我们检测数据中的异常值，如果在某个位置的累积和与预期相差较大，可能意味着该位置的数据存在问题，在财务审计中，通过计算发票金额的累积和，可以快速发现异常的发票。

移动平均

累积和可以用于计算移动平均值，移动平均值是一种平滑技术，可以减少数据的波动性，通过计算累积和，我们可以快速得到移动平均值，对于一个长度为n的窗口，第i个位置的移动平均值可以表示为：

[ text{移动平均值}_i = frac{text{cumsum}[i+n-1] text{cumsum}[i-1]}{n} ]

累计频率分布

在概率论和统计学中，累积频率分布是一种重要的工具，通过计算不同类别的累积频率，我们可以了解各类别的分布情况，在市场调研中，通过计算不同年龄段顾客的累积频率，可以了解顾客的年龄结构。

累积和的注意事项

虽然累积和是一个非常有用的工具，但在使用时也需要注意以下几点：

数据预处理

在使用累积和之前，需要确保数据的完整性和准确性，缺失值或异常值可能会影响累积和的结果，建议在进行累积和计算之前，先对数据进行清洗和预处理。

选择合适的窗口大小

在使用累积和进行移动平均时，选择合适的窗口大小非常重要，窗口过大会导致过度平滑，窗口过小则无法有效减少波动，通常需要根据具体问题和数据特点来确定合适的窗口大小。

注意边界条件

在计算累积和时，需要注意数组的边界条件，特别是当数组长度较短时，可能会导致累积和的结果超出数组范围，在编写代码时需要特别注意这一点。

相关问答FAQs

Q1: 如何计算一个数组的累积和？

A1: 可以使用NumPy库中的numpy.cumsum()函数来计算数组的累积和，示例代码如下：

import numpy as np
arr = np.array([1, 2, 3, 4, 5])
cumsum = np.cumsum(arr)
print(cumsum)

输出结果为[ 1 3 6 10 15]。

Q2: 累积和有哪些应用场景？

A2: 累积和在数据分析中有广泛的应用，包括数据趋势分析、异常值检测、移动平均和累计频率分布等，通过计算累积和，我们可以更好地理解数据的分布和趋势，从而做出更明智的决策。

小编有话说

累积和作为一种简单而有效的工具，在数据分析和统计学中有着广泛的应用，通过计算累积和，我们可以更好地理解数据的分布和趋势，从而做出更明智的决策，在使用累积和时，我们也需要注意数据的完整性和准确性，选择合适的窗口大小，并注意边界条件，希望本文能够帮助大家更好地理解和应用累积和这一工具。