性能测试的科学,它是如何工作的?
- 行业动态
- 2024-10-02
- 9
性能测试原理与技术原理
性能测试是衡量软件系统在特定负载条件下的性能表现的一系列活动,它主要关注系统的响应时间、吞吐量、资源利用率等关键指标,以确保系统能够在预期的工作负载下正常运行,性能测试的原理和技术原理主要包括以下几个方面:
1、性能测试的目标
性能测试的主要目标是确保软件系统在特定的负载条件下能够满足性能要求,包括响应时间、吞吐量、资源利用率等方面的要求,性能测试的目标包括:
确保系统在预期的负载下能够正常运行;
评估系统在不同负载条件下的性能表现;
发现系统可能存在的性能瓶颈和问题;
为系统优化提供依据。
2、性能测试的类型
性能测试可以分为多种类型,主要包括以下几种:
负载测试:模拟正常或峰值负载条件下的系统运行情况,评估系统在负载下的性能表现;
压力测试:模拟超过正常负载的极端条件,评估系统在压力下的性能表现和稳定性;
稳定性测试:长时间运行系统,评估系统的稳定性和可靠性;
容量测试:评估系统在最大负载条件下的性能表现,确定系统的容量限制;
并发测试:模拟多个用户同时访问系统,评估系统的并发处理能力。
3、性能测试的关键指标
性能测试的关键指标主要包括以下几个方面:
响应时间:指系统对请求的处理时间,通常用来衡量系统的响应速度;
吞吐量:指单位时间内系统处理的请求数量,反映系统的处理能力;
资源利用率:指系统资源的使用情况,如CPU、内存、磁盘等,用于评估系统资源的配置和使用效率;
并发用户数:指同时访问系统的用户数量,用于评估系统的并发处理能力;
事务率:指单位时间内系统完成的事务数量,用于评估系统的处理能力和性能。
4、性能测试的方法
性能测试的方法主要包括以下几种:
基准测试:通过对比不同配置下的系统性能,评估系统的性能差异;
仿真测试:使用仿真工具模拟真实场景,评估系统在实际应用中的性能表现;
实际测试:在实际环境中运行系统,评估系统在真实场景下的性能表现;
自动化测试:使用自动化测试工具进行性能测试,提高测试效率和准确性。
5、性能测试的工具
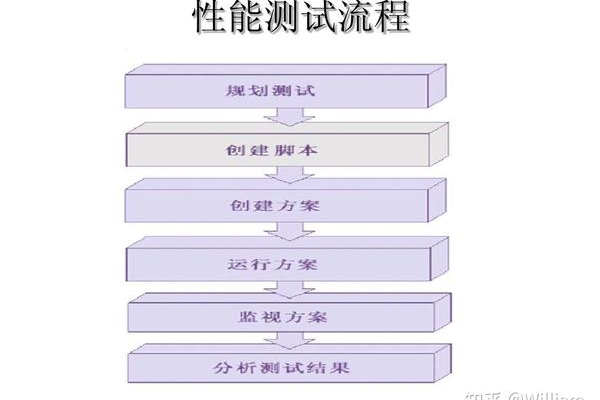
性能测试的工具主要包括以下几类:
负载生成器:用于模拟大量用户请求,如JMeter、LoadRunner等;
监控工具:用于实时监控系统资源使用情况,如Nagios、Zabbix等;
分析工具:用于分析性能测试结果,如Grafana、Kibana等;
报告工具:用于生成性能测试报告,如Allure、ExtentReports等。
相关问题与解答
问题1:如何选择合适的性能测试工具?
答:选择合适的性能测试工具需要考虑以下几个因素:
测试需求:根据测试目标和需求选择合适的工具;
工具功能:选择功能齐全、易于使用的工具;
工具支持的平台:选择支持所需操作系统和环境的工具;
工具的成本:考虑工具的价格和维护成本。
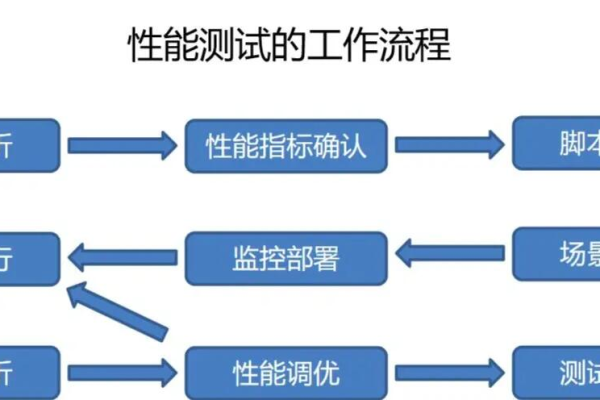
问题2:如何制定性能测试计划?
答:制定性能测试计划需要遵循以下步骤:
明确测试目标和需求:明确性能测试的目标和需求,以便有针对性地进行测试;
设计测试场景:根据实际应用场景设计测试场景,包括负载、压力、稳定性等方面;
选择测试工具:根据测试需求选择合适的性能测试工具;
编写测试用例:编写详细的测试用例,包括测试步骤、预期结果等;
安排测试时间和资源:合理安排测试时间和资源,确保测试顺利进行;
分析测试结果:对测试结果进行分析,找出性能瓶颈和问题;
优化系统:根据测试结果对系统进行优化,提高系统性能。
小伙伴们,上文介绍了“性能测试原理_技术原理”的内容,你了解清楚吗?希望对你有所帮助,任何问题可以给我留言,让我们下期再见吧。