如何查找QQ邮箱的邮件接收服务器信息?
- 行业动态
- 2024-09-08
- 4
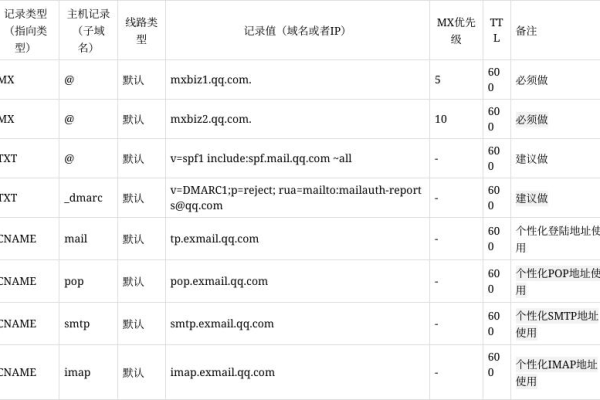
QQ邮箱的邮件接收服务器(POP3/IMAP)地址是
pop.qq.com (端口110)用于接收邮件,
imap.qq.com(端口143)用于同步邮件。
1、POP3服务器
服务器地址及端口:pop.qq.com,端口995。
SSL加密:使用SSL进行加密,保障邮件传输的安全性。
身份验证:在收取邮件时需要身份验证,通常使用邮箱密码或授权码作为验证方式。
适用范围:POP3协议适合只需要在单一设备上收取邮件的用户。
2、IMAP服务器
服务器地址及端口:imap.qq.com,端口993。
SSL支持:同样支持SSL,确保邮件内容在传输过程中的安全性。
邮件同步:IMAP协议允许用户在不同设备上访问邮件时,保持邮件的同步状态,更适合多设备使用的场景。

高效管理:IMAP协议还支持更高效的邮件管理,如创建文件夹、邮件排序等操作。
为了进一步帮助用户配置和使用QQ邮箱的邮件接收服务,以下是一些实用建议:
在使用POP3或IMAP协议前,确认已在QQ邮箱中开启相应的服务功能。
推荐使用授权码替代邮箱密码进行身份验证,以提高安全性。
根据个人需求选择适当的协议,若经常使用多个设备查看邮件,IMAP可能是更好的选择。
了解和配置正确的邮件接收服务器对于顺畅地使用电子邮件服务至关重要,通过上述信息,用户应能够有效地设置和管理自己的QQ邮箱账户,确保邮件的安全接收和高效管理。