服务器为何会显示错误信息?
- 行业动态
- 2024-11-09
- 3
服务器显示错误信息时,通常涉及多种类型和原因,以下是一些常见的服务器错误信息及其解释:
1、HTTP状态码
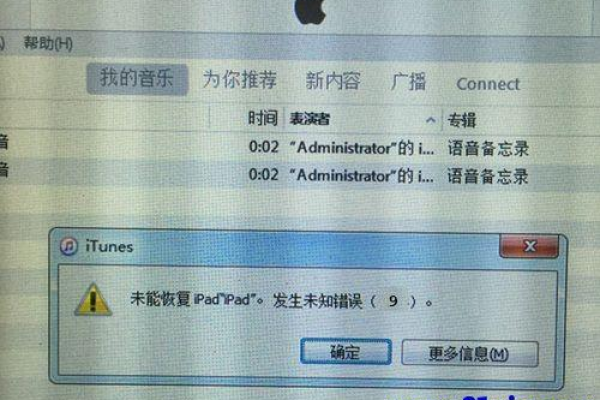
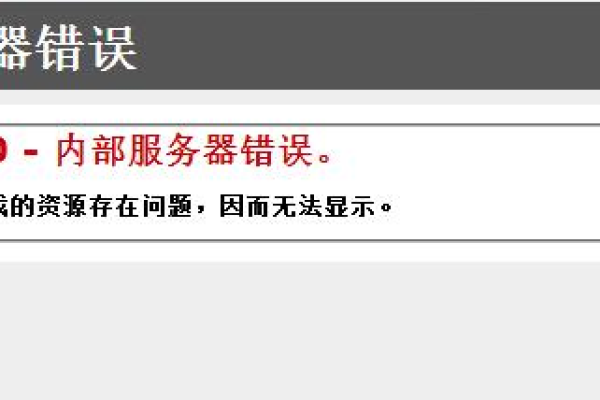
500 Internal Server Error(内部服务器错误):表示服务器遇到了意外的情况,无法完成请求,可能的原因包括配置错误、数据库故障、程序错误等。
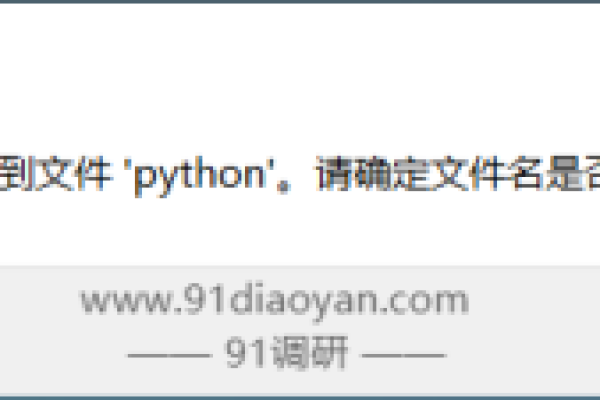
404 Not Found(找不到页面):服务器无法找到请求的页面或资源,可能的原因包括页面被删除、链接错误、文件路径错误等。
403 Forbidden(禁止访问):服务器拒绝了请求,不允许访问某个资源,可能的原因包括权限设置不正确、IP限制、访问控制列表等。
502 Bad Gateway(坏的网关):服务器作为网关或代理时无法从上游服务器获得有效的响应,可能的原因包括上游服务器错误、网络连接问题等。
503 Service Unavailable(服务不可用):服务器暂时无法提供请求的服务,可能的原因包括服务器过载、维护中、资源不足等。
2、错误代码与消息
错误代码:服务器错误会有对应的错误代码,例如HTTP状态码中的5xx系列错误。
错误消息:错误消息是服务器返回的详细错误信息,通常会告诉用户发生了什么问题,错误消息可能会提示数据库连接失败、文件权限错误或者程序异常等问题。
3、日志文件
错误日志:服务器错误还可能在错误日志中记录详细的错误信息,日志文件可以包含时间戳、请求细节、错误类型等有用信息,有助于分析和解决问题。
4、自定义页面
自定义错误页面:有些网站或应用程序会定义自己的错误页面,当发生服务器错误时会显示这些自定义页面,这些页面可以包含相关的错误信息和建议的解决办法。
5、调试信息
调试信息:在开发过程中,开发人员可以在服务器错误发生时显示调试信息,这些调试信息包括了错误发生的具体位置、错误的原因以及相关的变量值等。
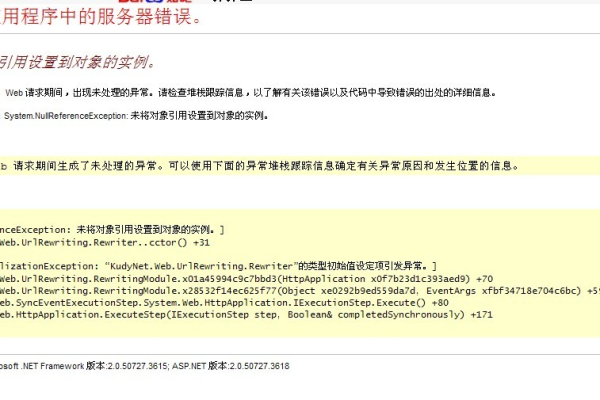
6、异常堆栈跟踪
异常堆栈跟踪:对于某些服务器错误,会生成一个异常堆栈跟踪,堆栈跟踪提供了一个错误的调用链,显示了错误是如何传播和导致服务器错误的。
服务器显示的错误信息种类繁多,每种错误都有其特定的含义和解决方案,通过理解这些错误信息,可以更有效地定位和解决问题,从而提高服务器的稳定性和用户体验。
以上内容就是解答有关“服务器显示错误信息”的详细内容了,我相信这篇文章可以为您解决一些疑惑,有任何问题欢迎留言反馈,谢谢阅读。