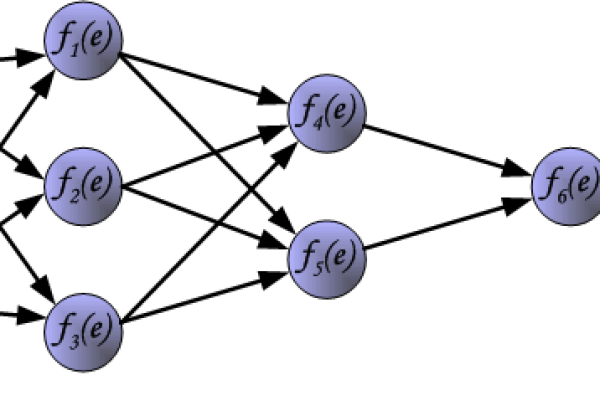
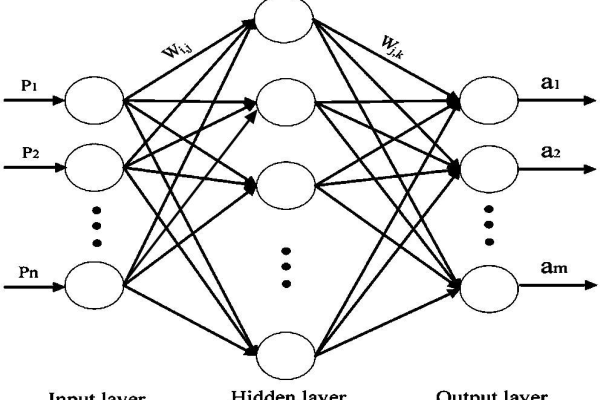
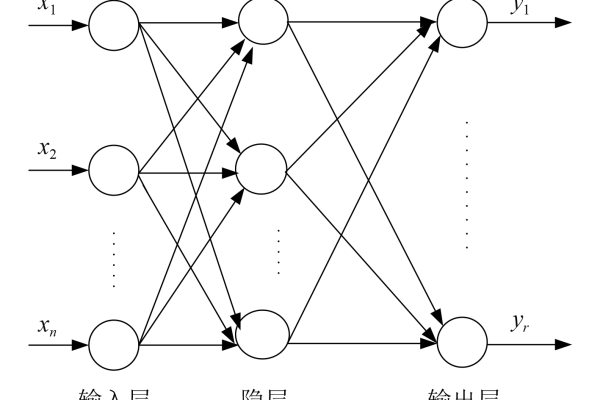
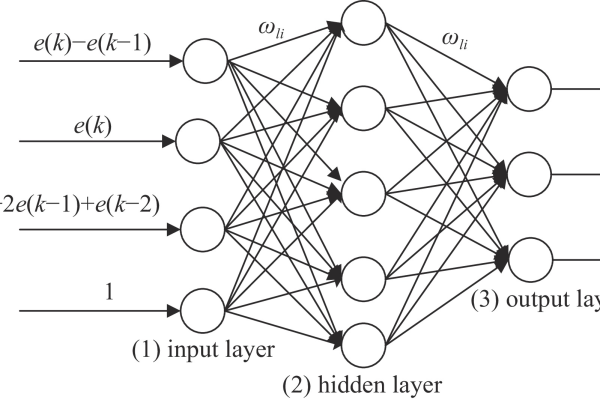
bp神经网络结构图

BP神经网络结构解析

什么是BP神经网络？

BP神经网络（Backpropagation Neural Network）是一种基于误差反向传播算法训练的多层前馈神经网络，其核心思想是通过输入数据的正向传播计算输出结果，再根据误差反向调整网络参数（权重和偏置），最终实现模型对数据的高精度拟合，它在分类、回归、模式识别等领域广泛应用，是深度学习的基础模型之一。

BP神经网络的结构图与组成

一个典型的三层BP神经网络结构图如下：

输入层      隐藏层      输出层
  ↓          ↓           ↓
X₁ → ○ → ○ → ○ → Y₁
X₂ → ○ → ○ → ○ → Y₂
X₃ → ○ → ○ → ○

输入层（Input Layer）

• 负责接收外部输入数据,神经元数量等于输入特征维度。
• 示例：若输入为RGB图像像素值（0-255），则输入层神经元数量为3（R/G/B通道）。

隐藏层（Hidden Layer）

• 用于提取数据的高阶特征,层数和神经元数量可自定义。
• 关键作用：通过激活函数（如Sigmoid、ReLU）实现非线性映射。
• 研究表明,单隐藏层网络即可逼近任意连续函数（Universal Approximation Theorem）。

输出层（Output Layer）

• 输出预测结果,神经元数量由任务类型决定：
  • 二分类：1个神经元（Sigmoid激活）
  • 多分类：神经元数=类别数（Softmax激活）
  • 回归：1个神经元（线性激活）

连接权重与偏置

• 权重（Weight）：决定各层神经元之间的连接强度。
• 偏置（Bias）：为神经元提供基础偏移量，增强模型灵活性。

BP神经网络的工作流程

前向传播（Forward Propagation）
数据从输入层经隐藏层逐层传递至输出层，计算公式：

• 隐藏层输出：$$hj = f(sum{i=1}^{n} w_{ij}x_i + b_j)$$
• 输出层结果：$$yk = g(sum{j=1}^{m} w_{jk}h_j + b_k)$$
  ( f )和( g )为激活函数，( w )为权重，( b )为偏置。

误差计算
通过损失函数（Loss Function）衡量预测值与真实值的差异，常用函数包括：

• 均方误差（MSE）：$$L = frac{1}{2}sum_{k=1}^{p}(y_k – hat{y}_k)^2$$
• 交叉熵损失（Cross-Entropy）：适用于分类任务。

反向传播（Backpropagation）
核心步骤：基于梯度下降法，反向调整权重与偏置。

• 计算输出层误差：$$delta_k = (y_k – hat{y}_k) cdot g'(z_k)$$
• 隐藏层误差：$$delta_j = f'(zj) cdot sum{k} deltak w{jk}$$
• 参数更新公式：
  $$w{jk} leftarrow w{jk} – eta cdot delta_k cdot h_j$$
  $$b_k leftarrow b_k – eta cdot delta_k$$
  （( eta )为学习率，控制参数更新步长）

BP神经网络的典型应用

1. 图像识别：手写数字分类（如MNIST数据集）
2. 自然语言处理：文本情感分析、机器翻译
3. 金融预测：股票价格趋势预测、风险评估
4. 工业控制：设备故障诊断、生产过程优化

BP神经网络的优势与局限

优势

• 强大的非线性拟合能力
• 可通过增加隐藏层处理复杂问题
• 算法成熟,训练工具丰富（如TensorFlow、PyTorch）

局限

• 易陷入局部最优解
• 训练速度受网络规模影响
• 需大量标注数据支持

引用说明

1. 经典教材《人工智能：现代方法》（Stuart Russell, Peter Norvig）第18章详细论述了反向传播算法的数学原理。
2. Rumelhart, Hinton与Williams于1986年在《Nature》发表的论文确立了BP算法的理论基础。
3. 工业级应用案例参考了Google的深度学习框架文档与Microsoft Azure的AI解决方案白皮书。