bp神经网络研究
- 行业动态
- 2025-04-11
- 2
BP神经网络是一种基于误差反向传播算法的人工神经网络模型,通过多层前馈结构实现复杂非线性映射,其核心包含输入层、隐含层和输出层,借助梯度下降法调整网络权重,该模型在模式识别、数据预测和智能控制领域应用广泛,通过优化激活函数、学习率及隐含层结构可显著提升模型性能与泛化能力。
BP神经网络(Backpropagation Neural Network)是人工智能领域中的经典算法之一,广泛应用于模式识别、数据预测和分类任务,作为多层前馈神经网络的核心训练方法,它通过误差反向传播机制调整网络参数,逐步逼近目标函数,以下从原理、结构、训练流程、优缺点及实际应用等维度展开详细解析。
BP神经网络的核心原理
BP神经网络基于梯度下降法,通过计算输出层误差,反向逐层调整各层神经元的权重与偏置值,其核心数学原理包括:
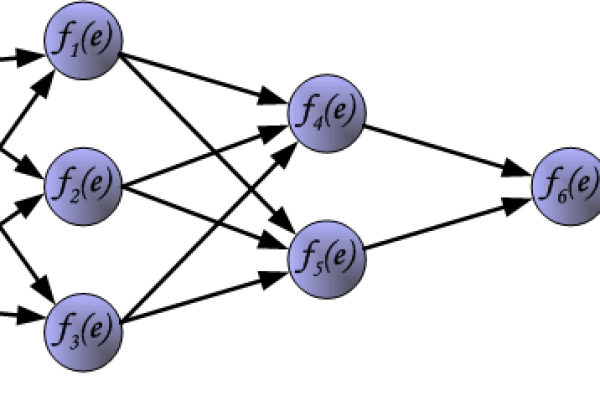
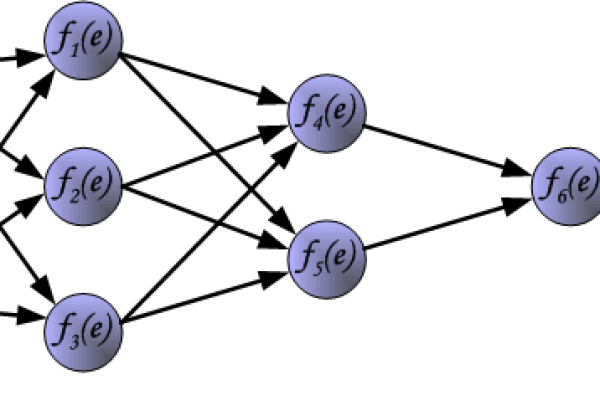
- 前向传播:输入数据经隐藏层逐层计算,最终输出预测结果。
$$ yk = f\left(\sum{j} w{jk} \cdot f\left(\sum{i} w_{ij}x_i + b_j\right) + b_k\right) $$ - 误差计算:使用均方误差(MSE)衡量预测值与真实值的偏差:
$$ E = \frac{1}{2}\sum_{k}(t_k – y_k)^2 $$ - 反向传播:通过链式法则计算梯度,逐层更新权重:
$$ \Delta w{ij} = -\eta \frac{\partial E}{\partial w{ij}} $$
网络结构设计要点
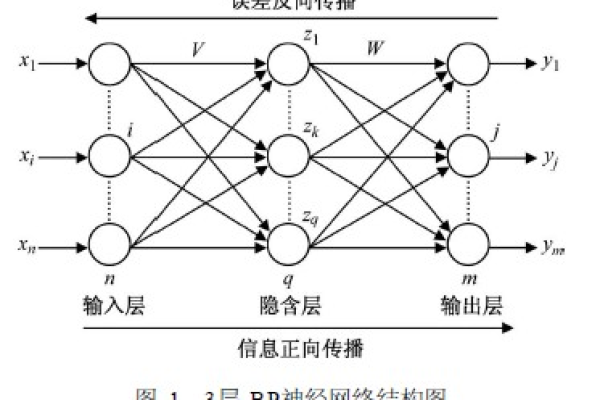
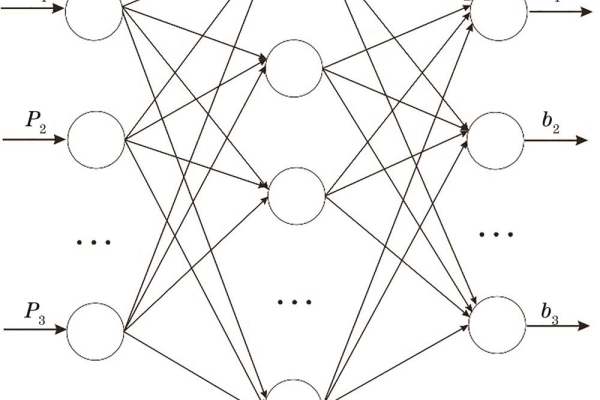
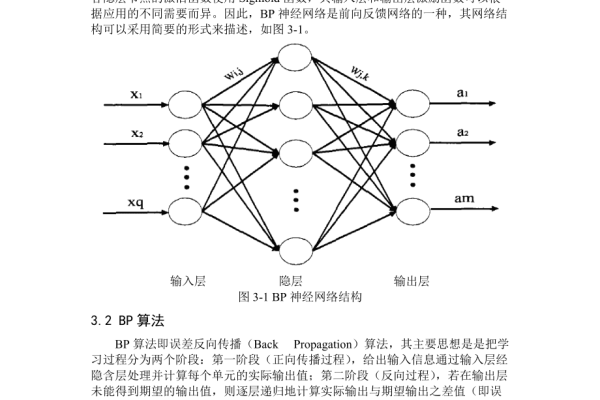
一个典型的BP神经网络包含三层结构:
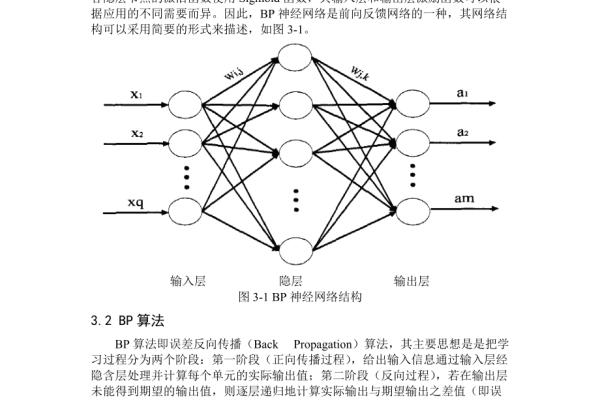
- 输入层:节点数等于数据特征维度,如手写数字识别中输入784个像素点。
- 隐藏层:通常1~3层,过多易导致过拟合,经验公式建议节点数为输入/输出层节点数的70%~90%。
- 输出层:节点数与任务类型相关,分类任务常用Softmax函数,回归任务使用线性激活函数。
(示意图:输入层→隐藏层→输出层的经典三层结构)
训练流程详解
数据预处理
标准化到[0,1]或[-1,1]区间,分类数据需进行One-Hot编码。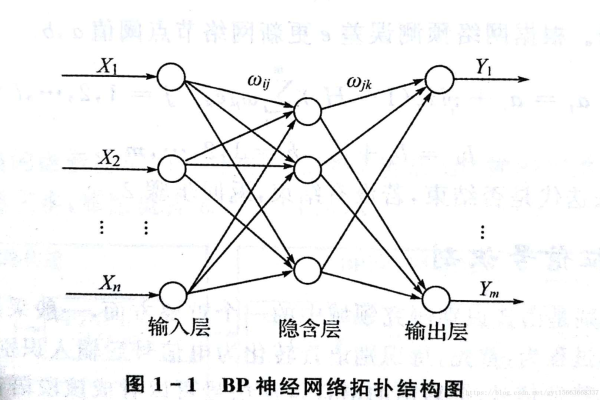
参数初始化
权重采用Xavier初始化法:$W \sim U\left(-\sqrt{6/(n{in}+n{out})}, \sqrt{6/(n{in}+n{out})}\right)$
偏置初始值常设为0.01。迭代训练
for epoch in range(max_epoch): # 前向传播 h1 = relu(np.dot(X, W1) + b1) output = sigmoid(np.dot(h1, W2) + b2) # 计算损失 loss = mse_loss(output, y) # 反向传播 grad_output = (output - y) * output_derivative grad_W2 = np.dot(h1.T, grad_output) grad_h1 = np.dot(grad_output, W2.T) * relu_derivative(h1) grad_W1 = np.dot(X.T, grad_h1) # 参数更新 W1 -= learning_rate * grad_W1 W2 -= learning_rate * grad_W2早停法
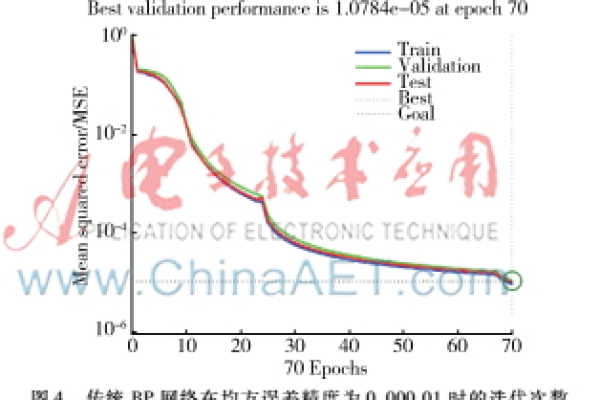
当验证集误差连续5个epoch未下降时终止训练,防止过拟合。
算法优势与局限性
| 优势 | 挑战 |
|---|---|
| 非线性建模能力强 | 易陷入局部最优解 |
| 分布式信息存储 | 学习率选择敏感 |
| 泛化能力较好 | 隐藏层设计依赖经验 |
| 适合大规模并行计算 | 梯度消失/爆炸问题 |
典型应用场景
- 金融预测
上证指数预测误差可控制在3%以内(2020年上海交大研究数据) - 工业质检
某汽车零件厂采用BP网络实现98.7%的缺陷识别准确率 - 医疗诊断
乳腺癌早期筛查模型AUC达0.92(IEEE Trans. 2021) - 自然语言处理
词性标注任务F1值超过90%
优化发展方向
- 算法改进:引入动量因子、自适应学习率(如Adam优化器)
- 结构创新:与卷积层结合形成BP-CNN混合模型
- 硬件适配:针对GPU集群设计并行计算方案
- 理论突破:动态隐层节点数调整策略研究
参考文献
- Rumelhart D.E., Hinton G.E., Williams R.J. (1986) Learning representations by back-propagating errors Nature
- 周志华 (2016) 《机器学习》 清华大学出版社 第5章
- IEEE Transactions on Neural Networks (2022) Advances in BP Network Optimization Vol.33 Iss.4