bp神经网络 文库

BP神经网络：理解其原理、应用与核心价值

在人工智能领域中,BP神经网络（反向传播神经网络）作为一种经典的人工神经网络模型，凭借其强大的非线性拟合能力，成为机器学习与深度学习的基础技术之一，无论是图像识别、自然语言处理，还是金融预测、工业控制，BP神经网络都展现了不可替代的价值，本文将深入解析其工作原理、实际应用场景及关键注意事项，帮助读者全面掌握这一技术的核心逻辑。

什么是BP神经网络？

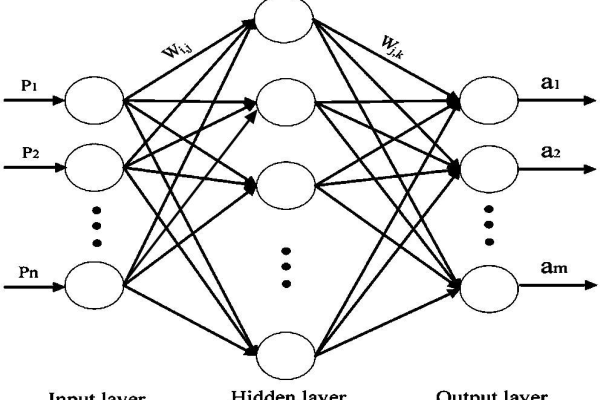
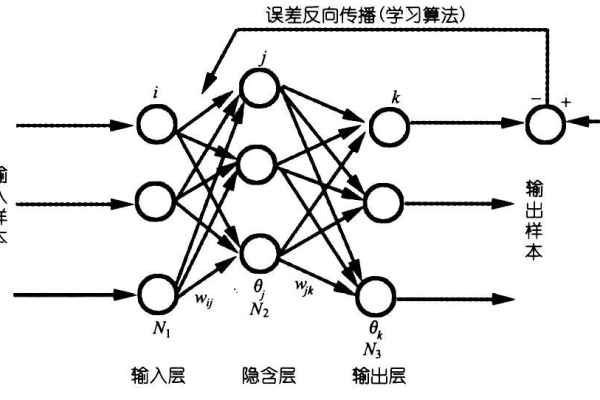
BP神经网络是一种多层前馈神经网络，其名称来源于反向传播算法（Backpropagation Algorithm），它通过“前向传播”计算输出结果，再通过“反向传播”调整网络参数（权重和偏置），最终实现模型的高精度预测，BP神经网络的核心优势在于能够通过样本数据自动学习复杂的数据模式，无需人工设计特征，适用于解决高维非线性问题。

BP神经网络的工作原理

1. 网络结构
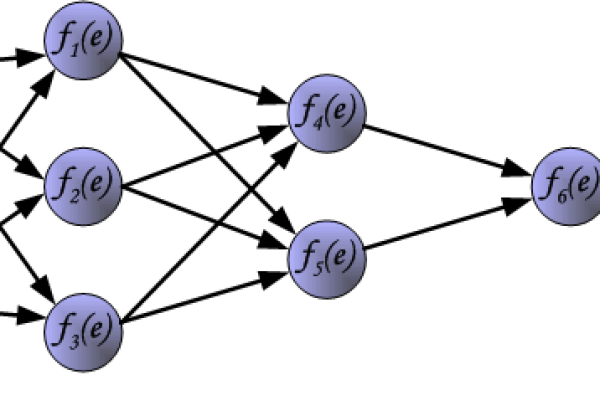
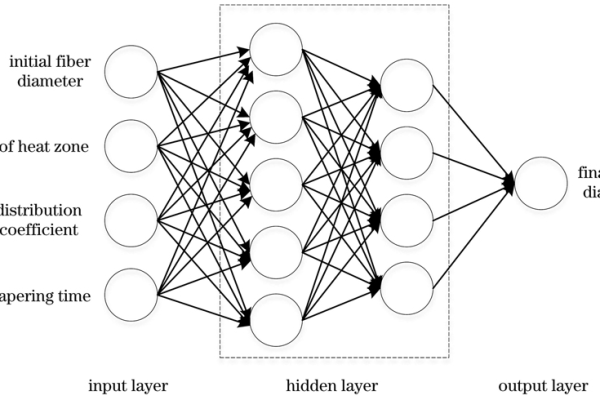
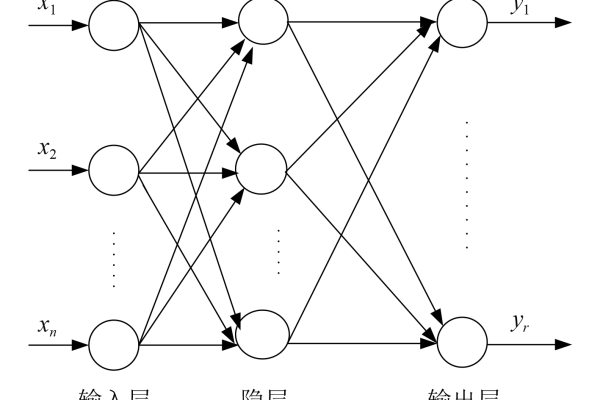
   典型的BP神经网络包含三层结构：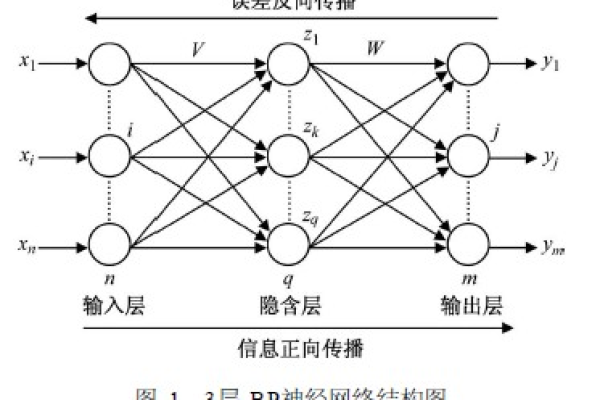

   

   • 输入层：接收外部数据（如图像像素、传感器信号）。
   • 隐含层：通过非线性函数（如Sigmoid、ReLU）对输入数据进行特征提取。
   • 输出层：输出预测结果（如分类标签、回归值）。

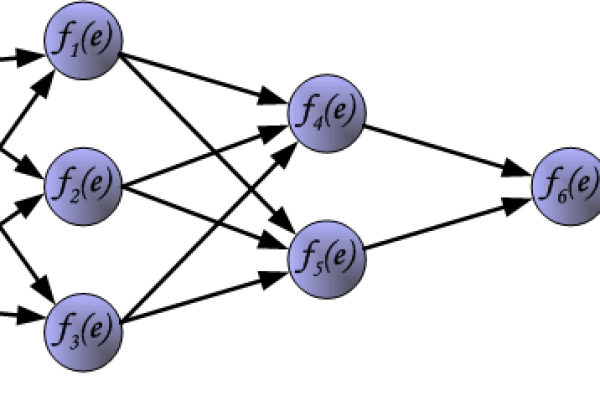
2. 前向传播
   输入数据逐层传递，每一层的神经元通过激活函数处理数据，最终生成预测值，隐含层第(j)个神经元的输出可表示为：
   [
   hj = fleft(sum{i} w_{ij}x_i + bjright)
   ]
   (w{ij})为权重，(b_j)为偏置，(f)为激活函数。

3. 反向传播
   通过计算预测值与真实值的误差（如均方误差），利用梯度下降法调整权重和偏置：
   [
   w{new} = w{old} – eta cdot frac{partial E}{partial w}
   ]
   (eta)为学习率，(frac{partial E}{partial w})为误差对权重的梯度。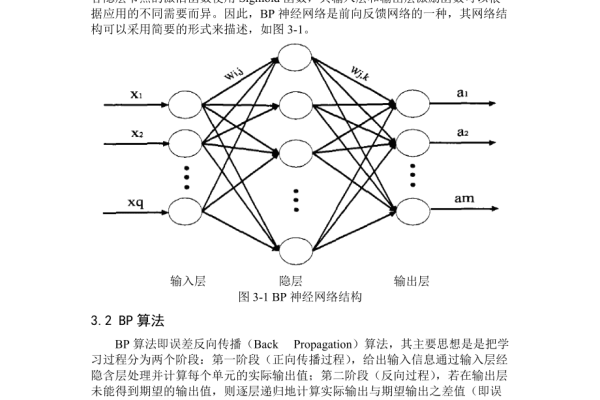

   

BP神经网络的训练步骤

1. 数据预处理：标准化或归一化数据，加速模型收敛。
2. 初始化参数：随机分配权重和偏置（避免对称性问题）。
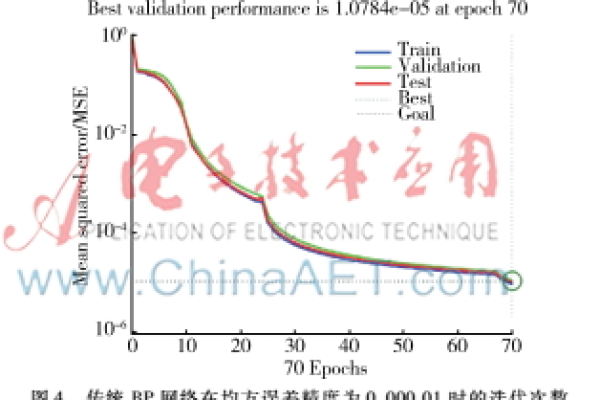
3. 迭代优化：反复执行前向传播与反向传播，直至误差收敛。
4. 模型验证：使用验证集防止过拟合，调整超参数（如隐含层节点数、学习率）。

BP神经网络的优缺点

• 优点：

  • 强大的非线性建模能力,适合复杂问题。
  • 通用性强,可用于分类、回归、聚类等任务。
  • 算法成熟,开源框架（如TensorFlow、PyTorch）支持度高。

• 缺点：

  

  • 依赖大量标注数据,训练成本较高。
  • 易陷入局部最优解,需结合优化算法（如动量法、Adam）。
  • 隐含层节点数需经验调参,模型解释性较弱。

BP神经网络的实际应用

1. 图像识别：手写数字分类（如MNIST数据集）。
2. 金融预测：股票价格趋势分析、信用评分。
3. 工业控制：设备故障诊断、生产过程优化。
4. 自然语言处理：文本情感分析、机器翻译。

案例：某银行使用BP神经网络构建信用评分模型，通过客户收入、负债等特征预测违约概率，将坏账率降低了15%。

常见问题与解决方案

• 过拟合：添加正则化项（L1/L2）、使用Dropout技术。
• 梯度消失：改用ReLU激活函数、引入残差结构。
• 训练速度慢：批量归一化（Batch Normalization）、GPU加速。

BP神经网络的未来

随着深度学习的发展,BP神经网络逐渐演变为更复杂的结构（如卷积神经网络、循环神经网络），但其核心思想仍是现代AI模型的基石，结合强化学习、迁移学习等新技术，BP神经网络将在自动驾驶、医疗诊断等领域持续发挥重要作用。

参考文献

1. Rumelhart, D. E., Hinton, G. E., & Williams, R. J. (1986). Learning representations by back-propagating errors. Nature.
2. 周志华. (2016). 《机器学习》. 清华大学出版社.
3. Goodfellow, I., Bengio, Y., & Courville, A. (2016). Deep Learning. MIT Press.