当前位置：首页 > 行业动态 > 正文

bp神经网络 权值阈值

BP神经网络通过调整权值和阈值优化网络性能， 权值决定神经元间连接强度， 阈值控制神经元激活状态，两者在反向传播过程中根据误差梯度逐层修正，从而最小化预测误差，提升模型拟合能力和分类精度。

BP神经网络中的权值与阈值：核心机制与优化策略

在BP神经网络（误差反向传播神经网络）中，权值（Weight）与阈值（Threshold）是决定模型性能的核心参数，它们的调整直接影响神经网络的预测精度、收敛速度及泛化能力，以下从定义、作用、调整方法及实际应用等角度展开详细说明。

权值与阈值的定义

  1. 权值（Weight）
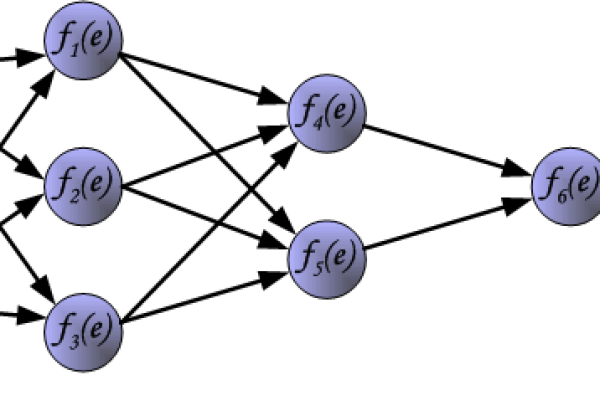
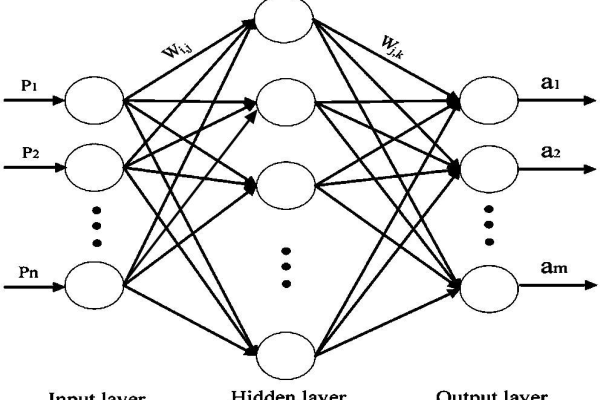
    权值是神经元之间连接的强度系数，表示输入信号对下一层神经元的影响程度，输入层到隐藏层的连接权值为 ( w_{ij} )，( i ) 代表前一层的神经元编号，( j ) 代表后一层的神经元编号。

  2. 阈值（Threshold）
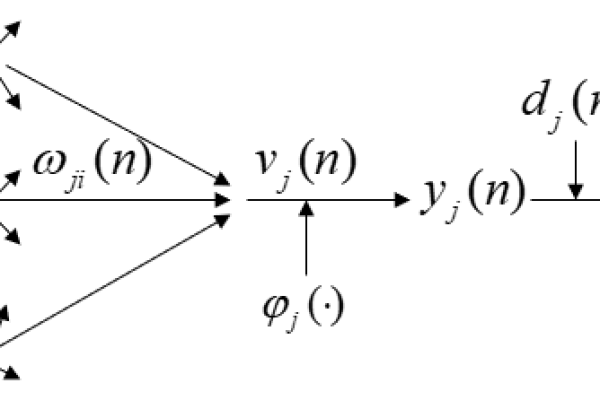
    阈值是神经元的激活门槛，通常与偏置（Bias）相关联，数学表达中，阈值体现为神经元输入的线性组合后的偏移量，( zj = sum w{ij}x_i + b_j )，( b_j ) 为阈值（偏置项）。

权值与阈值的作用

  1. 权值的作用

    bp神经网络 权值阈值

    • 信息传递强度：权值越大，对应的输入信号对下一层神经元的激活贡献越强。
    • 特征选择：通过调整权值，神经网络可自动筛选重要特征，抑制无关特征。
    • 模型复杂度控制：权值的分布决定网络的拟合能力，过大的权值可能导致过拟合。

  2. 阈值的作用

    • 激活调节：阈值决定神经元是否被激活，若加权和小于阈值，神经元输出可能为0。
    • 非线性引入：通过阈值与激活函数（如Sigmoid、ReLU）结合，模型可学习复杂的非线性关系。

权值与阈值的调整方法

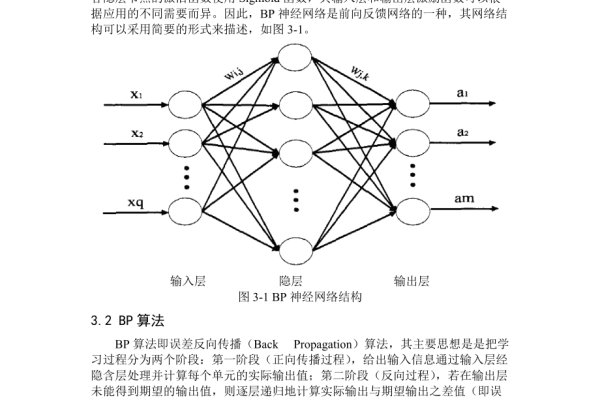
BP神经网络通过反向传播算法优化权值与阈值，核心步骤包括：

  1. 前向传播
    输入数据逐层计算，得到预测输出，公式为：
    [
    a^{(l)} = f(z^{(l)}), quad z^{(l)} = W^{(l)}a^{(l-1)} + b^{(l)}
    ]
    ( f ) 为激活函数，( W^{(l)} )、( b^{(l)} ) 分别为第 ( l ) 层的权值与阈值。

  2. 误差计算
    通过损失函数（如均方误差、交叉熵）衡量预测值与真实值的差距。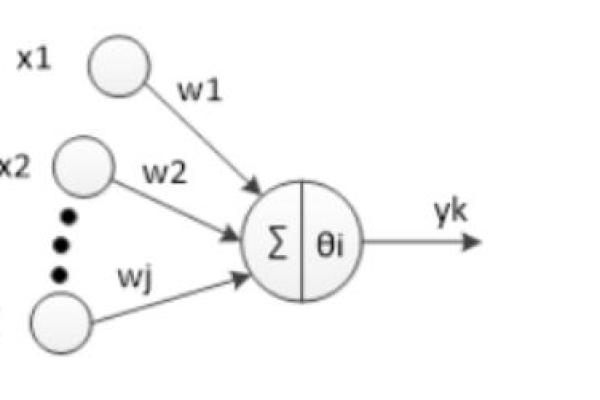

    bp神经网络 权值阈值

  3. 反向传播梯度
    按链式法则逐层计算权值与阈值的梯度：
    [
    frac{partial L}{partial W^{(l)}} = delta^{(l)} cdot a^{(l-1)}, quad frac{partial L}{partial b^{(l)}} = delta^{(l)}
    ]
    ( delta^{(l)} ) 为第 ( l ) 层的误差项。

  4. 参数更新
    使用梯度下降法更新参数：
    [
    W^{(l)} leftarrow W^{(l)} – eta frac{partial L}{partial W^{(l)}}, quad b^{(l)} leftarrow b^{(l)} – eta frac{partial L}{partial b^{(l)}}
    ]
    ( eta ) 为学习率。

权值与阈值的初始化策略

良好的初始化可加速收敛并避免梯度消失/爆炸问题：

  • 随机初始化：权值初始化为小随机数（如均值为0、方差为0.01的正态分布）。
  • Xavier初始化：针对激活函数选择权值范围，例如对Tanh函数，权值方差设置为 ( 1/n )（( n ) 为输入维度）。
  • 阈值初始化：通常设为0或小常数。

实际应用中的注意事项

  1. 过拟合问题
    • 通过L1/L2正则化约束权值大小。
    • 采用Dropout随机屏蔽部分神经元。
  2. 学习率调整

    自适应学习率算法（如Adam、RMSProp）可动态调整参数更新幅度。

    bp神经网络 权值阈值

  3. 批量归一化

    对输入数据或隐藏层输出进行归一化，减少阈值调整的依赖。

权值与阈值是BP神经网络中“可学习”的核心参数，二者的协同优化决定了模型的最终表现，通过合理的初始化、梯度下降法及正则化技术，可显著提升网络性能，实际应用中需结合具体任务调整策略，例如图像分类可能需更深的网络与复杂权值约束，而时序预测则需关注阈值的动态调节。

引用说明

  1. Rumelhart, D. E., Hinton, G. E., & Williams, R. J. (1986). Learning representations by back-propagating errors. Nature.
  2. Goodfellow, I., Bengio, Y., & Courville, A. (2016). Deep Learning. MIT Press.
  3. Glorot, X., & Bengio, Y. (2010). Understanding the difficulty of training deep feedforward neural networks. AISTATS.
BP神经网络权值阈值

相关文章