bp神经网络神经元函数
- 行业动态
- 2025-04-11
- 2
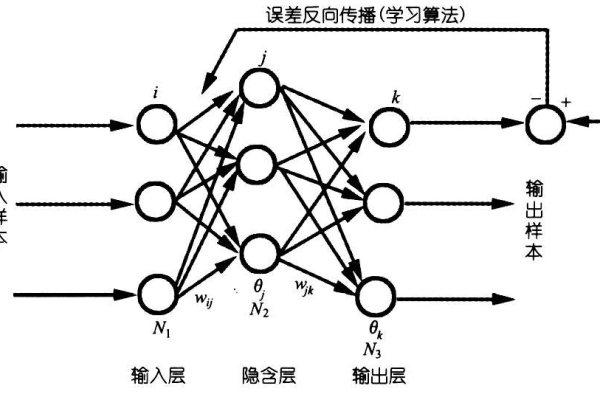
BP神经网络通过误差反向传播调整神经元连接权重,其核心是
神经元激活函数,常用Sigmoid、ReLU等非线性
函数处理输入信号,实现输入到输出的复杂映射,激活函数引入非线性特性,直接影响网络的学习能力和收敛速度,是构建多层感知机的关键组件。
BP神经网络中的神经元函数:深度解析与应用
在BP神经网络(误差反向传播神经网络)中,神经元函数(又称激活函数)是模型的核心组件之一,直接影响网络的非线性表达能力、训练速度及最终性能,本文将从原理、类型、选择原则及实际应用角度,详细解析BP神经网络中神经元函数的作用与意义。
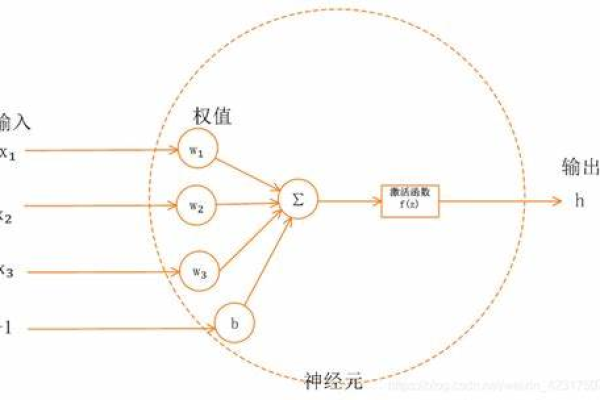
神经元函数的作用
神经元函数位于神经元的输出端,负责将输入信号的加权和转换为输出值,其核心作用包括:
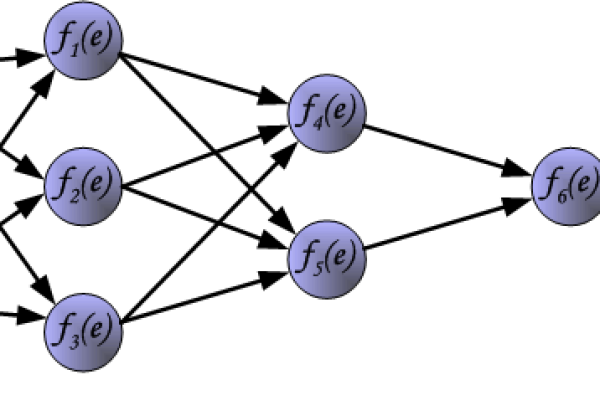
- 引入非线性:若没有非线性激活函数,多层神经网络将退化为单层线性模型,无法处理复杂问题(如图像分类、自然语言处理)。
- 控制输出范围:通过函数特性(如Sigmoid将输出压缩至0-1),保证信号在合理范围内传递。
- 梯度传播:激活函数的导数影响反向传播中梯度的计算,进而决定模型收敛速度。
常见神经元函数及特性
以下是BP神经网络中常用的激活函数,各具优缺点,需根据任务需求选择:
Sigmoid函数
- 数学公式:
( f(x) = frac{1}{1 + e^{-x}} ) - 输出范围:0到1
- 优点:平滑易求导,适合概率输出(如二分类)。
- 缺点:
- 梯度消失问题(两侧饱和区导数趋近0);
- 输出非零中心化,影响梯度下降效率。
Tanh函数(双曲正切函数)
- 数学公式:
( f(x) = frac{e^x – e^{-x}}{e^x + e^{-x}} ) - 输出范围:-1到1
- 优点:零中心化,缓解梯度偏移问题;比Sigmoid梯度更强。
- 缺点:仍存在梯度消失问题。
ReLU函数(修正线性单元)
- 数学公式:
( f(x) = max(0, x) ) - 输出范围:0到正无穷
- 优点:
- 计算高效,解决梯度消失(正区间导数为1);
- 加速收敛,广泛用于隐藏层。
- 缺点:
- 神经元“死亡”问题(负输入梯度为0);
- 输出非零中心化。
Leaky ReLU函数
- 数学公式:
( f(x) = begin{cases} x, & x geq 0 alpha x, & x < 0 end{cases} )((alpha)通常取0.01) - 优点:缓解ReLU的神经元死亡问题,负区间保留微小梯度。
- 缺点:需手动调参(alpha),效果因任务而异。
Softmax函数
- 数学公式:
( f(x_i) = frac{e^{xi}}{sum{j=1}^n e^{x_j}} ) - 输出范围:0到1(多分类概率分布)
- 应用场景:专用于多分类输出层,与交叉熵损失函数配合使用。
选择神经元函数的关键原则
- 任务类型:
- 输出层:回归任务常用线性函数,二分类用Sigmoid,多分类用Softmax。
- 隐藏层:优先ReLU及其变体(如Leaky ReLU),兼顾效率与性能。
- 梯度特性:
避免梯度消失或爆炸,如深层网络慎用Sigmoid/Tanh。 - 计算复杂度:
ReLU的计算速度远高于Sigmoid,适合大规模数据。 - 稀疏性需求:
ReLU可产生稀疏激活,减少参数依赖。
实际应用中的优化策略
- 初始化配合:使用He初始化(ReLU)或Xavier初始化(Sigmoid/Tanh),匹配激活函数特性。
- 批归一化(Batch Norm):缓解梯度问题,允许更灵活的函数选择。
- 组合使用:深层网络中,混合ReLU(隐藏层)+ Softmax(输出层)是常见方案。
参考文献
- Ian Goodfellow, Yoshua Bengio, Aaron Courville. Deep Learning. MIT Press, 2016.
- Glorot, X., & Bengio, Y. (2010). Understanding the difficulty of training deep feedforward neural networks. AISTATS.
- Nair, V., & Hinton, G. E. (2010). Rectified linear units improve restricted boltzmann machines. ICML.
通过合理选择神经元函数,开发者能显著提升BP神经网络的性能与效率,实践中需结合具体场景,通过实验验证最佳方案。