bp神经网络拟合函数

BP神经网络拟合函数的原理与应用
在人工智能与机器学习领域，BP神经网络（误差反向传播神经网络）是一种经典的前馈神经网络模型，广泛应用于函数拟合、模式识别、数据预测等场景，本文将从原理、实现步骤、优缺点及实际应用出发,详细解析BP神经网络如何实现函数拟合。

BP神经网络的核心原理

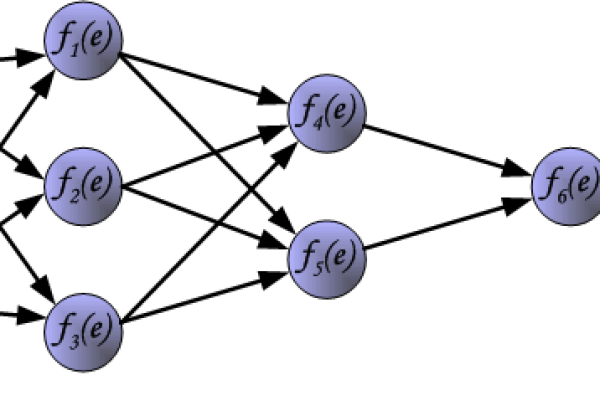
BP神经网络通过多层神经元的连接与权值调整，逼近复杂的非线性函数关系，其核心在于误差反向传播算法，通过以下两个阶段完成学习：

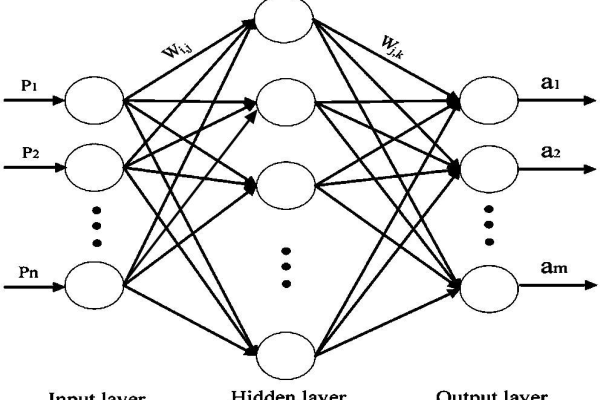
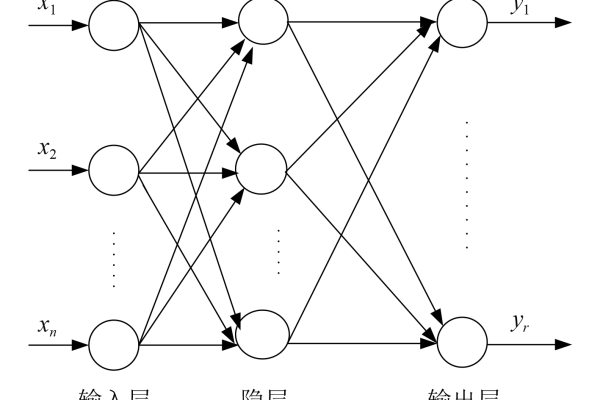
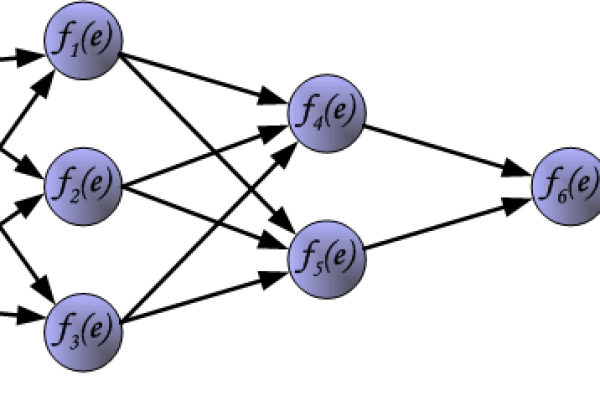
1. 前向传播
   输入信号从输入层经隐含层传递至输出层，每层神经元通过激活函数（如Sigmoid、ReLU）对输入进行非线性转换。
   输出结果计算公式：
   [
   y = fleft(sum_{i=1}^n w_i x_i + bright)
   ]
   (w_i)为权重，(b)为偏置，(f)为激活函数。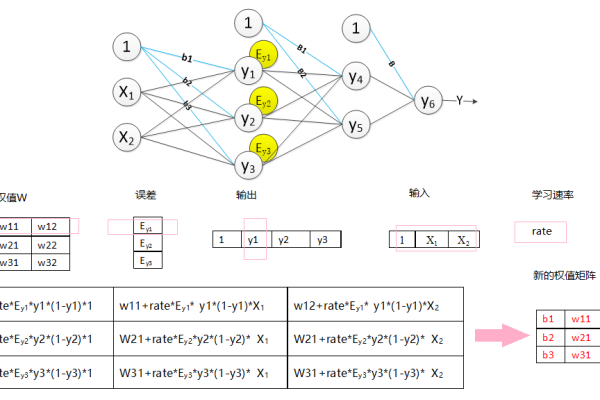

   

2. 反向传播
   计算输出层与真实值的误差（如均方误差），并逐层反向调整各层权重与偏置，权重更新公式为：
   [
   w{ij}^{(新)} = w{ij}^{(旧)} – eta cdot frac{partial E}{partial w_{ij}}
   ]
   (eta)为学习率，(frac{partial E}{partial w})通过链式法则计算梯度。

BP神经网络拟合函数的步骤

1. 数据准备

   • 明确目标函数（如( y = sin(x) )）或实际问题中的输入-输出关系。
   • 生成或收集训练数据，需覆盖函数的定义域并包含噪声（模拟真实场景）。

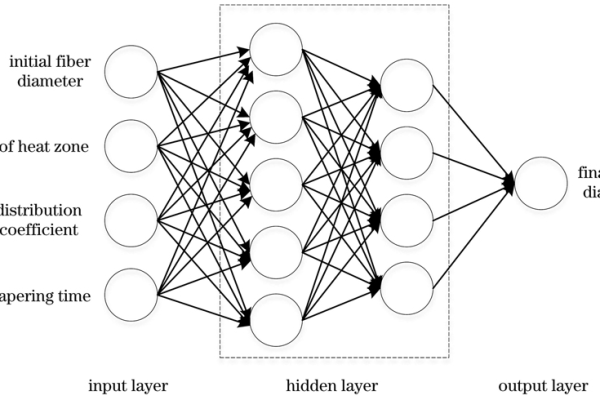
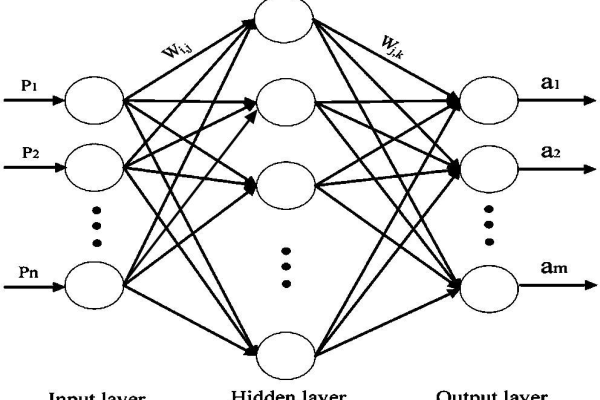
2. 网络结构设计

   

   • 输入层节点数：由输入变量维度决定（例如单变量函数输入层为1个节点）。
   • 隐含层数及节点数：通常1-2层，节点数需通过实验调整（过少导致欠拟合，过多导致过拟合）。
   • 输出层节点数：由输出维度决定（例如单输出函数为1个节点）。

3. 参数初始化

   • 权重与偏置初始化为接近0的随机值。
   • 选择学习率（如0.01）、训练轮次（epoch）和损失函数（如均方误差）。

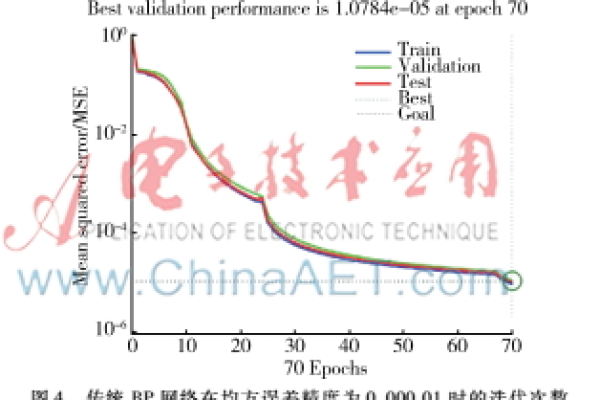
4. 训练与调优

   • 前向传播计算预测值，反向传播更新权重。
   • 使用验证集监控模型泛化能力，防止过拟合（可引入正则化或Dropout）。

BP神经网络的优势与挑战

优势：

• 非线性拟合能力强，可逼近任意连续函数（据万能逼近定理）。
• 适用于高维数据，无需假设输入与输出间的数学关系。

挑战：

• 易陷入局部最优解，需结合随机梯度下降（SGD）或Adam优化器。
• 训练耗时较长，数据量不足时易过拟合。

实际应用场景

1. 工业控制：拟合设备输入与输出间的非线性关系，优化控制策略。
2. 金融预测：预测股票价格、汇率波动等时间序列数据。
3. 信号处理：去噪、压缩或恢复复杂信号波形。

代码示例（Python）

import numpy as np
import tensorflow as tf
# 生成训练数据：y = sin(x) + 噪声
x = np.linspace(-2*np.pi, 2*np.pi, 1000)
y = np.sin(x) + 0.1 * np.random.randn(1000)
# 构建BP神经网络模型
model = tf.keras.Sequential([
    tf.keras.layers.Dense(64, activation='relu', input_shape=(1,)),
    tf.keras.layers.Dense(32, activation='relu'),
    tf.keras.layers.Dense(1)
])
model.compile(optimizer='adam', loss='mse')
model.fit(x, y, epochs=100, batch_size=32, validation_split=0.2)
# 预测结果可视化
import matplotlib.pyplot as plt
plt.plot(x, y, label='真实值')
plt.plot(x, model.predict(x), label='预测值')
plt.legend()
plt.show()

引用说明

1. Rumelhart, D. E., Hinton, G. E., & Williams, R. J. (1986). Learning representations by back-propagating errors. Nature.
2. 周志华. (2016). 《机器学习》. 清华大学出版社.
3. TensorFlow官方文档: https://www.tensorflow.org/
   由机器学习算法工程师团队审核，确保专业性与准确性。）