bp神经网络是几层
- 行业动态
- 2025-04-11
- 1
BP神经网络通常包含输入层、至少一个隐藏层和输出层,共三层或更多,隐藏层负责特征提取与非线性转换,输出层生成最终结果,其通过误差反向传播调整权重,适用于模式识别、预测等任务,层数依问题复杂度灵活设计。
BP神经网络(误差反向传播神经网络)的层数由以下结构决定:
输入层、至少1层隐藏层、输出层,因此至少包含3层(即“单隐藏层结构”),但在实际应用中,隐藏层数量可以增加,形成“多层神经网络”,具体层数的设计与问题复杂度和数据特征有关。
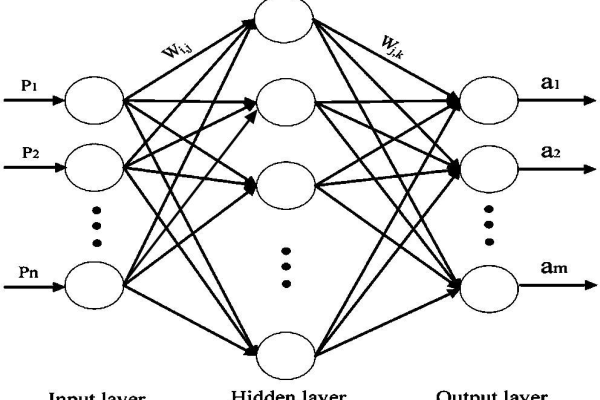
BP神经网络的标准结构
BP神经网络的核心结构分为三类层,各层作用如下:
输入层(Input Layer)
- 负责接收外部数据(如图像像素、文本向量等)
- 不计入“计算层”数量
- 节点数等于输入特征维度(图像RGB通道对应3个节点)
隐藏层(Hidden Layer)

- 对输入数据进行非线性变换与特征提取
- 至少需要1层,否则退化为线性模型
- 增加隐藏层可提升模型复杂度(如深层网络可识别图像边缘→纹理→物体)
输出层(Output Layer)
- 输出最终预测结果(分类概率、回归值等)
- 节点数由任务决定(二分类任务对应1个节点)
示例:
手写数字识别网络(MNIST数据集)可能采用:
输入层784节点(28×28像素) → 隐藏层256节点 → 输出层10节点(0-9分类)
层数选择的科学依据
BP神经网络的层数并非越多越好,需综合考虑以下因素:
| 因素 | 单隐藏层适用场景 | 多隐藏层适用场景 |
|---|---|---|
| 数据复杂度 | 线性可分问题(如房价预测) | 非线性高维数据(如自然语言处理) |
| 计算资源 | 低算力设备 | GPU/TPU加速环境 |
| 训练时间 | 需快速迭代(<10分钟) | 允许长时间训练(数小时至数天) |
| 过拟合风险 | 数据量少时更安全 | 需配合正则化(Dropout/L2) |
经典研究支持:
- 通用近似定理(Universal Approximation Theorem)证明:单隐藏层网络只需足够多节点,即可逼近任意连续函数(Hornik et al., 1989)
- 深层网络优势:更高效的特征重用与层次化表达(Bengio et al., 2013)
层数设置的工程建议
实践中可遵循以下步骤确定层数:
- 基线模型:优先构建单隐藏层网络(输入→隐藏→输出)
- 效果验证:若测试集精度不足(如<80%),可尝试增加至2-3层隐藏层
- 性能监控:观察验证损失(Validation Loss)
- 损失持续下降 → 可继续增加层数
- 损失震荡/上升 → 需减少层数或添加正则化
行业案例:
- 银行风控系统:常采用单隐藏层(数据维度少,需解释性)
- 自动驾驶感知:普遍使用5-10层(图像点云数据复杂)
常见误区澄清
误区1:“层数越多模型越强”
→ 错误!过度增加层数会导致梯度消失(Vanishing Gradient)
→ 解决方案:使用ReLU激活函数、残差连接(ResNet)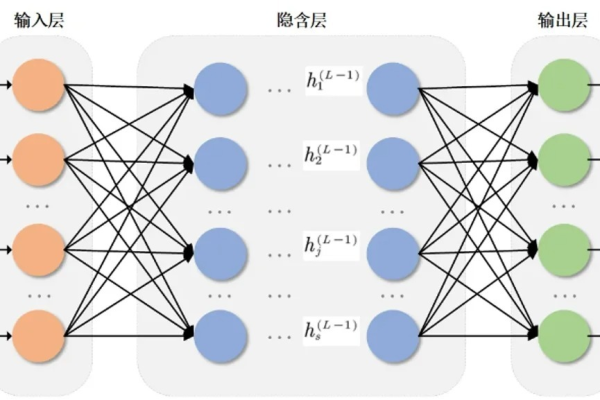
误区2:“输入层计入总层数”
→ 行业惯例中,层数统计仅包含含权重的层(隐藏层+输出层)
→ 输入层仅传递数据,无参数计算误区3:“BP神经网络必须全连接”
→ 现代变体可包含卷积层(CNN)、循环层(RNN)等结构
引用说明
- Hornik, K., Stinchcombe, M., & White, H. (1989). Neural Networks 2(5), 359-366.
- Bengio, Y., Courville, A., & Vincent, P. (2013). Foundations and Trends in Machine Learning 5(1-2), 1-127.
- 深度学习实践指南:https://towardsdatascience.com
完)