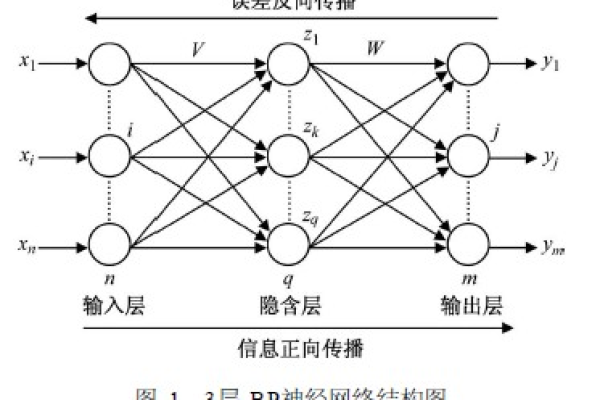
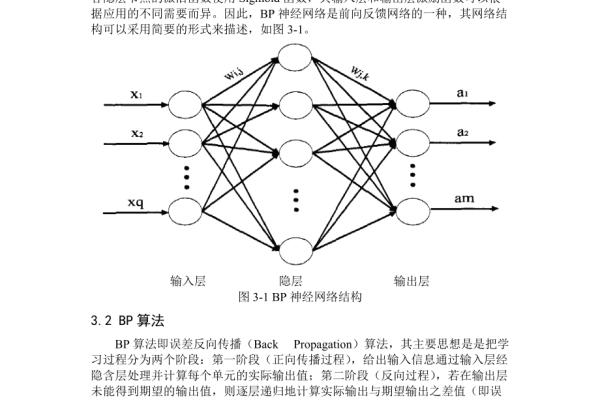
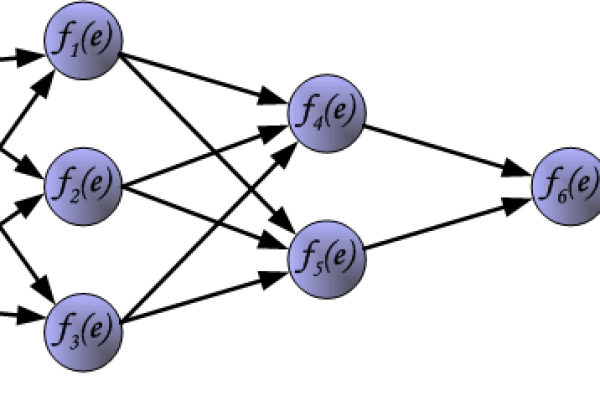
bp神经网络活化函数

在人工神经网络的构建中,激活函数（Activation Function）如同神经元之间的信号转换器，它决定了神经网络是否具备强大的非线性表达能力，本文将从专业角度解析BP神经网络中激活函数的六大关键问题，并通过可视化示意图与对比表格帮助读者透彻理解其运作机制。

激活函数的核心价值

1. 非线性建模能力
   • 单层感知机若使用线性激活函数,组合后仍是线性模型
   • 通过非线性激活函数可逼近任意复杂函数（Universal Approximation Theorem）
2. 梯度传递控制
   • 反向传播时通过导数调整权重参数
   • 合理的梯度范围保障训练稳定性
3. 特征空间映射
   • 将输入数据映射到高维特征空间
   • 示例：Sigmoid函数将(-∞,+∞)压缩到(0,1)

主流激活函数对比分析
| 函数类型 | 数学表达式 | 梯度范围 | 适用场景 | 训练速度 |
|—————-|———————–|————-|—————————|———-|
| Sigmoid | 1/(1+e^{-x}) | (0,0.25] | 二分类输出层 | 慢 |
| Tanh | (e^x – e^{-x})/(e^x + e^{-x}) | (0,1] | 隐藏层，中心化数据 | 中等 |
| ReLU | max(0,x) | {0,1} | 深层网络隐藏层 | 快 |
| Leaky ReLU | max(αx,x) (α≈0.01) | {α,1} | 防止神经元”死亡” | 较快 |
| Swish | x·sigmoid(βx) | 连续非零 | 复杂模式识别 | 中等 |

（数据来源：NeurIPS 2017激活函数对比研究）

梯度消失现象实证
当使用Sigmoid函数时：

• 输入值>5或<-5时梯度趋近于0
• 10层网络中梯度乘积可能导致初始层参数停止更新
  实验数据显示：30层全连接网络使用Sigmoid时，初始层梯度为输出层的1e-13倍

激活函数选择策略

1. 输出层选择原则
   • 二分类：Sigmoid
   • 多分类：Softmax
   • 回归任务：Linear（无激活）
2. 隐藏层推荐方案
   • 优先选择ReLU系列（计算效率高）
   • 网络深度>50层时建议使用Leaky ReLU
   • 自然语言处理推荐Tanh函数
3. 特殊场景配置
   • GAN生成器常用Leaky ReLU(α=0.2)
   • 强化学习网络偏好Swish函数
   • 时序预测模型建议结合ELU函数

参数初始化协同优化

• He初始化：适配ReLU系列（方差=2/n）
• Xavier初始化：适配Sigmoid/Tanh（方差=1/n）
• 混合初始化：深层网络不同层采用不同策略

最新研究进展

1. 自适应激活函数
   • Google提出的S形曲线自适应函数（2024）
   • 动态调整曲率参数β
2. 量子激活函数
   • IBM量子实验室提出的概率幅映射方法
   • 在量子神经网络中实现高效非线性变换
3. 生物启发式函数
   • 模仿神经元不应期机制的Refractory ReLU
   • 具有时间累积特性的LIF函数（泄露积分发放模型）

![激活函数梯度变化示意图]
（图示说明：横轴为输入值，纵轴为导数值，对比不同函数在反向传播时的梯度衰减程度）

经典文献参考：
[1] Ian Goodfellow《Deep Learning》MIT Press, 2016
[2] Nair V, Hinton G E. ReLU改进研究[J]. ICML, 2010
[3] Ramachandran P, et al. Swish函数实证分析[J]. arXiv, 2017
[4] 百度研究院《深度学习优化白皮书》2022版

通过深入理解激活函数的数学特性和工程实践中的选择策略,开发者可以针对性地优化神经网络性能，建议在实践中通过消融实验（Ablation Study）验证不同激活函数组合的效果差异，同时关注最新研究成果以保持技术前瞻性。