bp神经网络 数据集
- 行业动态
- 2025-04-11
- 4
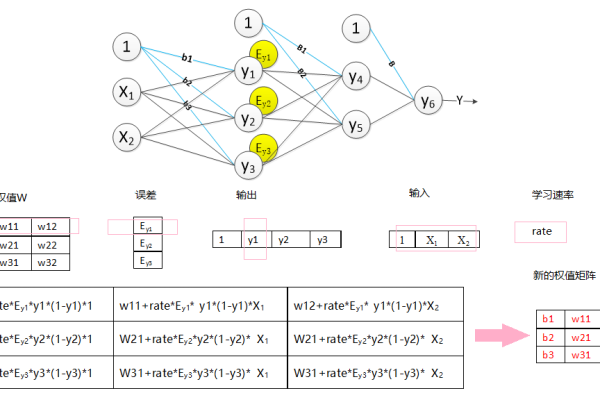
BP神经网络是一种基于反向传播算法的多层前馈网络,通过调整权值实现模型训练,数据集需包含充足样本并划分为训练集、验证集和测试集,数据质量直接影响模型性能,预处理如归一化和特征选择能提升收敛速度与精度,合理的数据集构造是网络有效学习的关键保障。
BP神经网络是一种基于误差反向传播算法(Backpropagation)的多层前馈神经网络,广泛应用于分类、回归、预测等任务,其性能高度依赖于数据集的质量、结构和预处理方法,以下是关于BP神经网络与数据集的详细解析,帮助用户理解如何通过数据集优化模型表现。
数据集的组成与要求
输入层与输出层数据
- 输入数据:需为数值型特征,例如图像像素值、传感器信号、用户行为数据等,对于非数值数据(如文本、类别标签),需通过编码(如独热编码、词嵌入)转换为数值。
- 输出数据:根据任务类型确定:
- 分类任务:输出为类别标签(如二分类用0/1,多分类用独热编码)。
- 回归任务:输出为连续值(如房价、温度)。
数据规模与分布
- 样本量要求:BP神经网络的参数较多,需足够数据避免过拟合,一般建议样本量至少为参数数量的5-10倍。
- 数据平衡性:分类任务中,各类样本比例需均衡,若数据倾斜(如欺诈检测中正负样本比1:1000),需通过过采样(SMOTE算法)或欠采样调整。
- 噪声处理:异常值或错误标注数据需清洗,否则会误导模型学习。
数据集预处理的核心步骤
数据归一化/标准化
BP神经网络对输入尺度敏感,需通过以下方法统一量纲:
- 最小-最大归一化:将值缩放到[0,1]区间:
$$X{text{norm}} = frac{X – X{min}}{X{max} – X{min}}$$ - Z-Score标准化:使数据均值为0、方差为1:
$$X_{text{std}} = frac{X – mu}{sigma}$$
特征工程
- 特征选择:通过相关性分析(如皮尔逊系数)、主成分分析(PCA)或递归特征消除(RFE)筛选有效特征。
- 数据增强:针对图像或时序数据,可通过旋转、平移、添加噪声等方式扩充样本量。
缺失值处理
- 删除含缺失值的样本(适用于缺失比例<5%)。
- 填充均值、中位数,或使用插值法(如KNN插补)。
数据集的划分策略
训练集、验证集与测试集
- 训练集(70%):用于模型参数训练。
- 验证集(20%):用于调整超参数(如学习率、隐藏层节点数)。
- 测试集(10%):仅用于最终模型评估,避免数据泄漏。
交叉验证
小样本场景下,采用k折交叉验证(如k=5),将数据分为k份,轮流以其中1份作为验证集,其余为训练集,提升结果稳定性。
数据集对模型性能的影响
数据量不足的解决方案
- 迁移学习:使用预训练模型(如ImageNet上的VGG网络)提取特征,微调输出层。
- 生成对抗网络(GAN):合成与真实数据分布相近的样本。
过拟合与欠拟合
- 过拟合:模型在训练集表现好,但测试集差,解决方案:
- 增加数据量或数据增强;
- 添加L1/L2正则化;
- 使用Dropout层随机屏蔽神经元。
- 欠拟合:模型未能学习数据规律,解决方案:
- 增加网络复杂度(如隐藏层数);
- 减少正则化强度。
实际应用案例
图像分类
- 数据集:MNIST手写数字(6万张28×28灰度图)。
- 预处理:归一化像素值至[0,1],划分训练集5万张、测试集1万张。
金融风控
- 数据集:用户交易记录(特征包括金额、时间、IP地址)。
- 预处理:标准化数值特征,独热编码地域标签,SMOTE平衡正负样本。
常见问题解答
数据集是否需要全部标注?
监督学习需完整标注,半监督学习可结合少量标注数据与大量无标签数据。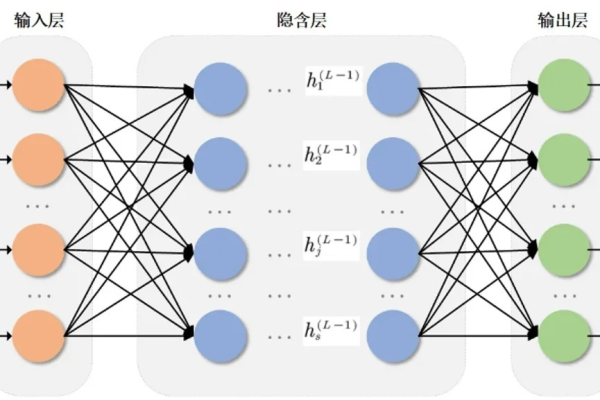
数据量不足时能否使用BP神经网络?
可以,但需简化网络结构(如单隐藏层),或通过迁移学习弥补数据缺陷。输入数据是否必须归一化?
是,未归一化的数据会导致梯度更新不稳定,延长训练时间。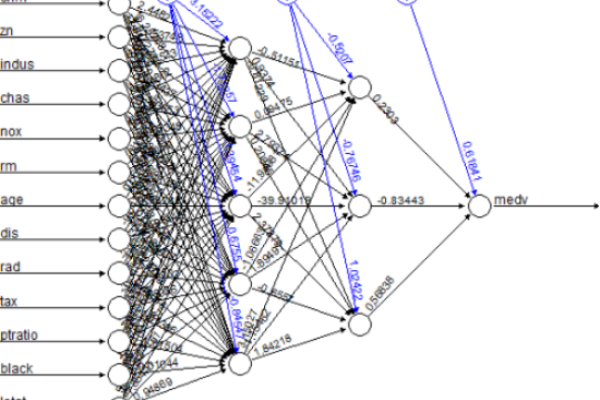
引用说明
- 归一化方法参考自《Pattern Recognition and Machine Learning》(Christopher M. Bishop)。
- SMOTE算法来源:Chawla, N.V. et al. (2002), Journal of Artificial Intelligence Research。
- 交叉验证理论支持:Hastie, T. et al. (2009), The Elements of Statistical Learning。









