bp神经网络的预测模型

BP神经网络（反向传播神经网络）是一种经典的人工神经网络模型，广泛应用于预测、分类和模式识别等领域，其核心思想基于“误差反向传播”机制，通过不断调整网络参数，使模型输出尽可能接近真实值，以下将从原理、构建步骤、应用场景及优化方向全面解析BP神经网络的预测模型。

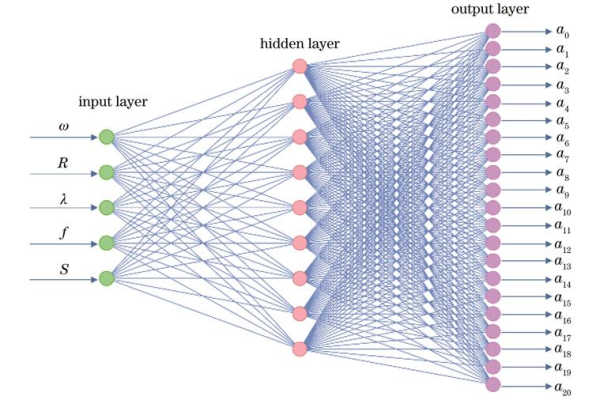
BP神经网络的基本原理

BP神经网络由输入层、隐含层和输出层构成，每层包含若干神经元，通过激活函数实现非线性映射,训练过程分为两个阶段：

1. 前向传播
   输入数据经过加权求和与激活函数处理，逐层传递至输出层,生成预测结果。
2. 反向传播
   计算预测结果与真实值的误差，利用梯度下降算法逐层调整权重和偏置，最小化损失函数（如均方误差MSE）。

数学表达示例
假设隐含层激活函数为Sigmoid，输出层为线性函数，则输出层结果：
$$ yk = \sum{j=1}^{m} w{jk} \cdot \sigma\left( \sum{i=1}^{n} w_{ij}x_i + b_j \right) + bk $$
$w{ij}$为输入层到隐含层的权重，$b_j$为偏置，$\sigma$为Sigmoid函数。

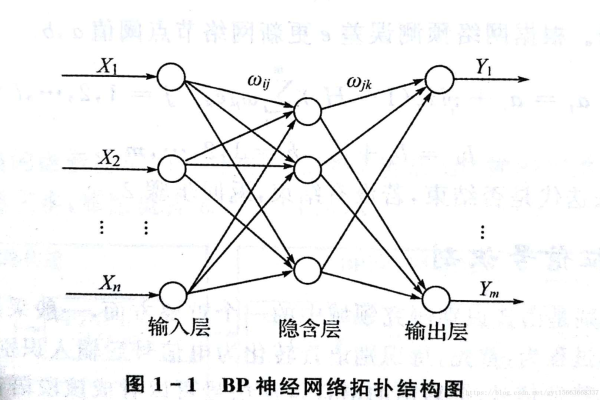
BP神经网络预测模型的构建步骤

数据准备与预处理

• 数据清洗：处理缺失值、异常值。
• 归一化：将数据缩放到[0,1]或[-1,1],避免量纲差异影响训练。
• 数据集划分：按比例（如7:2:1）分为训练集、验证集和测试集。

网络结构设计

• 输入层节点数：与特征维度一致（如房价预测包含面积、位置等5个特征，则节点数为5）。
• 隐含层设计：通常1-2层，节点数可通过经验公式或试错法确定（如$\sqrt{n+m}+a$，$n$为输入节点数，$m$为输出节点数，$a$为1~10的常数）。
• 输出层节点数：由预测目标决定（如单输出回归问题为1，多分类问题为类别数）。

模型训练

• 参数初始化：权重通常随机初始化为[-0.5, 0.5]的小数。
• 学习率选择：过大易震荡，过小收敛慢，建议从0.01开始调整。
• 迭代终止条件：达到最大迭代次数（如1000次）或误差低于阈值（如1e-5）。

模型评估与优化

• 评估指标：回归任务用MAE、RMSE；分类任务用准确率、F1值。
• 避免过拟合：采用Dropout、L2正则化或早停法（Early Stopping）。
• 超参数调优：利用网格搜索（Grid Search）或贝叶斯优化调整隐含层数和节点数。

BP神经网络预测模型的应用场景

1. 金融领域
   股票价格预测、信用评分、风险评估。
2. 工业控制
   设备故障预警、生产工艺参数优化。
3. 医疗健康
   疾病诊断（如糖尿病预测）、药物疗效分析。
4. 能源与环境
   电力负荷预测、空气质量指数（AQI）预测。

案例说明
某电商平台使用BP神经网络预测用户购买行为，输入特征包括浏览时长、历史消费、页面点击量等，输出为购买概率，模型准确率达89%,助力精准营销。

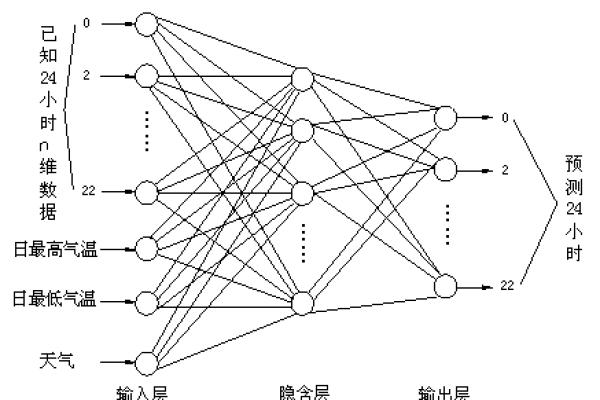
BP神经网络的挑战与改进方向

1. 局部极小值问题
   引入动量项（Momentum）或Adam优化器,跳出局部最优。
2. 训练速度慢
   采用批量归一化（Batch Normalization）或GPU加速。
3. 数据依赖性强
   结合卷积神经网络（CNN）或长短期记忆网络（LSTM）处理时空数据。

参考文献

1. 周志华. 《机器学习》. 清华大学出版社, 2016.（原理与优化方法）
2. Bishop C M. 《Pattern Recognition and Machine Learning》. Springer, 2006.（数学推导与案例）
3. 实验代码库：GitHub开源项目（如TensorFlow、PyTorch官方示例）.