bp 网络拓

在人工智能与机器学习领域，BP神经网络（误差反向传播神经网络）的拓扑结构是经典模型之一，其设计和应用对深度学习发展具有深远影响，以下内容将从核心概念、拓扑结构、工作原理、优缺点及实际应用场景展开详细解析,帮助读者全面理解这一技术。

BP神经网络的核心概念

BP神经网络是一种多层前馈神经网络，通过误差反向传播算法（Back Propagation）进行权重调整，实现对复杂非线性关系的建模，其名称中的“BP”即指该算法通过输出层误差反向逐层调整网络参数的特性。

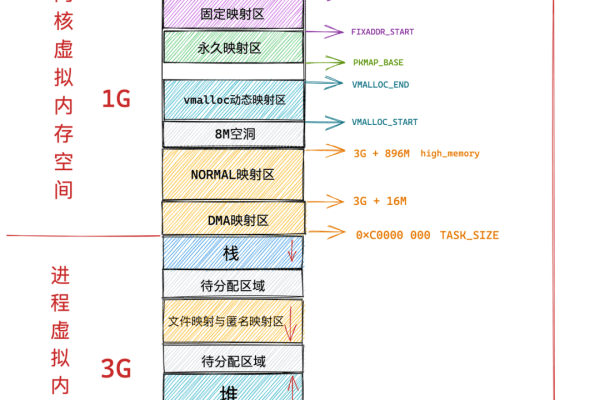
BP神经网络的拓扑结构

BP神经网络的拓扑结构由输入层、隐含层（可多级）和输出层构成，各层之间通过全连接方式传递信号。

1. 输入层：接收外部数据，节点数通常对应特征维度。
   示例：图像识别任务中，输入节点数等于图像的像素数。
2. 隐含层：负责提取数据特征，层数和节点数需根据任务复杂度调整。
   经验法则：隐含层数越多，网络表达能力越强，但也可能引发过拟合。
3. 输出层：生成最终预测结果，节点数由输出类型决定。
   二分类任务通常使用1个节点（Sigmoid函数），多分类则用Softmax函数。

（示意图：典型的三层BP网络结构）

BP神经网络的工作原理

1. 前向传播
   输入信号从输入层经隐含层逐层加权传递，最终在输出层计算预测值，公式为：
   [
   yk = f\left( \sum{j} w{jk} \cdot f\left( \sum{i} w_{ij} x_i + bj \right) \right)
   ]
   ( w{ij} )为权重，( b_j )为偏置项，( f )为激活函数（如Sigmoid、ReLU）。

2. 误差反向传播
   计算输出层误差后，通过梯度下降法逐层调整权重与偏置：
   [
   \Delta w{ij} = -\eta \cdot \frac{\partial E}{\partial w{ij}}
   ]
   ( \eta )为学习率，( E )为损失函数（如均方误差、交叉熵）。

   

BP神经网络的优缺点

优势：

• 强大的非线性拟合能力，适用于图像识别、金融预测等复杂任务。
• 算法通用性强，易于与其他模型结合（如卷积层、递归结构）。

局限性：

• 易陷入局部极小值，需结合动量法、自适应学习率优化。
• 训练时间长，尤其是深层网络。
• 对初始权重敏感，需合理初始化（如Xavier、He方法）。

实际应用场景

1. 模式识别
   手写数字识别（MNIST数据集）、人脸检测。
2. 金融预测
   股票价格趋势分析、信用评分模型。
3. 工业控制
   设备故障诊断、生产过程优化。
4. 自然语言处理
   文本分类、情感分析（需结合词嵌入技术）。

优化BP网络的关键技巧

• 数据预处理：归一化或标准化输入数据，加速收敛。
• 正则化：L2正则化、Dropout防止过拟合。
• 批量训练：使用Mini-batch梯度下降平衡速度与稳定性。
• 自适应优化器：Adam、RMSProp替代传统梯度下降。

参考文献

1. Rumelhart, D. E., Hinton, G. E., & Williams, R. J. (1986). Learning representations by back-propagating errors. Nature.
2. 周志华. (2016). 机器学习. 清华大学出版社.
3. Goodfellow, I., Bengio, Y., & Courville, A. (2016). Deep Learning. MIT Press.

通过以上内容，读者可系统掌握BP神经网络的拓扑结构及核心原理，在实际使用中，建议结合具体任务调整网络深度与参数，并借助现代框架（如TensorFlow、PyTorch）提升开发效率。