如何从零开始注册您的首个域名网站?
- 行业动态
- 2024-10-11
- 6
选择域名
选择一个合适的域名对于网站的品牌建设和SEO优化都至关重要,以下是一些选择域名的建议:
1、简短易记:域名应尽量简短,便于用户记忆和输入。
2、相关性:域名最好与网站内容或品牌相关,有助于提升品牌形象和搜索引擎排名。
3、避免使用连字符:虽然连字符可以帮助区分不同的单词组合,但它们也可能让用户感到困惑,增加输入错误的风险。
4、考虑扩展名:常见的域名扩展名包括.com、.org、.net等。.com是最受欢迎和最广泛认可的扩展名,但也要考虑其他可能更适合您网站内容的扩展名。
查找域名可用性
在确定好域名后,需要检查该域名是否已被注册,可以通过以下方式进行查找:
1、直接访问域名注册商网站:大多数域名注册商都提供在线搜索功能,可以快速查询域名的可用性。
2、使用WHOIS查询工具:WHOIS是一个用于查询域名注册信息的数据库,通过WHOIS查询工具,可以了解某个域名的所有者、注册日期等信息,从而判断该域名是否可用。
选择域名注册商
选择一个可靠的域名注册商非常重要,在选择时,可以考虑以下因素:
1、价格:比较不同注册商的价格,选择性价比高的。
2、服务质量:查看用户评价,了解注册商的客户服务和技术支持质量。
3、附加服务:一些注册商可能提供额外的服务,如隐私保护、电子邮件托管等,这些服务可能对您有用。

注册域名流程
一旦选择了域名和注册商,就可以开始注册流程了,注册流程包括以下几个步骤:
1、搜索并选择域名:在注册商网站上搜索您想要的域名,如果可用,则将其添加到购物车。
2、填写注册信息:根据要求填写域名所有者的信息,包括姓名、地址、电话等,这些信息将被公开显示在WHOIS数据库中(除非您购买了隐私保护服务)。
3、选择注册年限:通常可以选择1年、2年或更长的注册期限,长期注册通常更划算。
4、支付费用:完成支付后,域名将正式被您注册。
5、确认注册成功:注册成功后,您将收到一封确认邮件,其中包含您的域名信息和管理面板链接。
设置DNS
DNS(域名系统)负责将域名转换为IP地址,以便浏览器能够找到并加载相应的网站,在注册域名后,您需要设置DNS记录,以便将您的域名指向您的网站服务器,具体步骤如下:
1、登录域名管理面板:使用注册时提供的用户名和密码登录域名管理面板。
2、找到DNS设置选项:在管理面板中找到“DNS设置”或类似的选项。

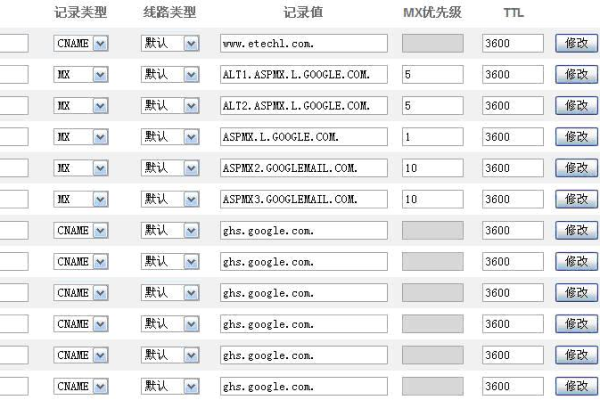
3、添加DNS记录:根据您的网站服务器提供商的要求,添加相应的A记录、CNAME记录、MX记录等,如果您的网站托管在阿里云上,您可能需要添加一个A记录,将域名指向阿里云分配给您的IP地址。
4、保存更改:完成DNS设置后,点击“保存”按钮,注意,DNS更改可能需要一些时间才能生效,通常需要等待几分钟到几小时不等。
后续管理
注册域名后,您还需要定期进行一些管理工作,以确保域名的安全和有效运行,以下是一些建议:
1、更新联系信息:确保您的联系信息(如电子邮件地址、电话号码等)是最新的,以便在需要时能够及时接收到通知。
2、续费域名:在域名到期前及时续费,以避免域名被删除或被他人抢注。
3、监控域名安全:定期检查域名的状态和安全设置,确保没有未经授权的更改。
相关问题与解答
问题1:如何选择一个合适的域名?
答:选择一个合适的域名需要考虑多个因素,包括长度、相关性、易记性和扩展名等,一个好的域名应该简短、易于拼写和记忆,同时与您的网站内容或品牌相关,还需要考虑目标受众的语言和文化背景,以及域名的发音和含义是否容易理解。

问题2:注册域名后需要做什么?
答:注册域名后,您需要进行以下操作:
设置DNS记录,将域名指向您的网站服务器。
确保联系信息是最新的,以便在需要时能够及时接收到通知。
定期检查域名的状态和安全设置,确保没有未经授权的更改。
在域名到期前及时续费,以避免域名被删除或被他人抢注。
以上就是关于“初学者怎么注册域名网站”的问题,朋友们可以点击主页了解更多内容,希望可以够帮助大家!