如何使用TeamViewer手机版远程控制电脑?
- 行业动态
- 2024-10-10
- 6
下载TeamViewer手机版并安装,打开应用后输入电脑端的ID和密码即可远程控制。
TeamViewer手机版远程控制电脑使用教程
下载与安装
1. 手机端
步骤:打开应用商城,搜索“TeamViewer”,选择官方应用进行下载并安装。
2. 电脑端
步骤:访问TeamViewer官网(https://www.teamviewer.com),下载与电脑操作系统匹配的版本并进行安装。
启动与连接
1. 启动应用
步骤:在手机和电脑上分别启动TeamViewer应用。
2. 获取连接信息
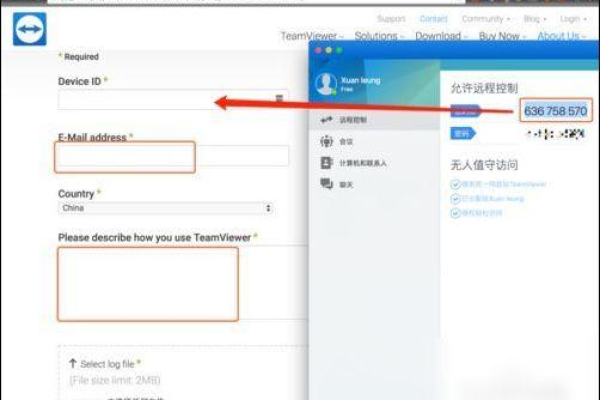
步骤:在电脑端,你会看到一个唯一的ID和一个随机生成的密码,这些信息是连接的关键。
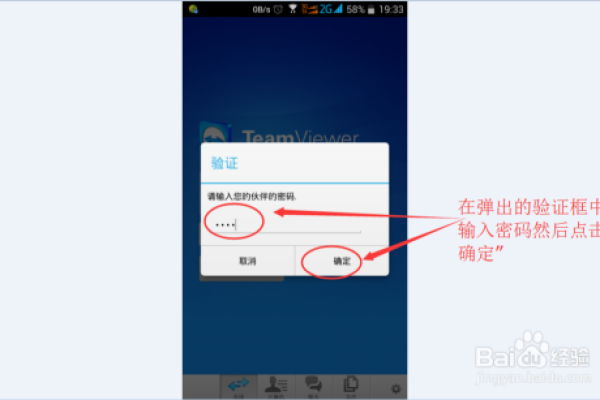
3. 输入ID与密码
步骤:在手机上的TeamViewer应用中,点击“远程控制”或“远程支持”功能,输入电脑上的ID,并点击“连接”,输入电脑上显示的密码。

4. 设置无人值守访问密码(可选)
步骤:为了方便,可以设置一个无人值守访问密码,在电脑版TeamViewer主界面中,点击个人密码输入框里的画笔图标,自定义一个密码。
常见问题与解答
问题1:如果连接时提示密码错误怎么办?
答案1:请确保输入的密码正确无误,注意区分大小写,如果还是无法连接,可以尝试重启TeamViewer软件重新获取新的密码。
问题2:如何设置无人值守访问密码?
答案2:在电脑版TeamViewer主界面中,点击个人密码输入框里的画笔图标,自定义一个密码,设置完成后,就可以使用这个密码进行无人值守的远程控制了。
通过以上步骤,您应该能够顺利地在手机上远程控制您的电脑,如果在操作过程中遇到任何问题,可以参考TeamViewer的官方文档或联系其客服支持。
以上就是关于“TeamViewer手机版远程控制电脑使用教程”的问题,朋友们可以点击主页了解更多内容,希望可以够帮助大家!