当前位置：首页 > 行业动态 > 正文

bp神经网络 权值调整

BP神经网络权值调整

在人工神经网络领域，反向传播(BP)神经网络是最经典且应用最广泛的模型之一，BP神经网络通过权值调整来实现对复杂非线性关系的建模能力,这一过程是神经网络学习的核心机制。

权值调整的基本原理

BP神经网络的权值调整基于误差反向传播算法，其核心思想是通过梯度下降法最小化网络输出与期望输出之间的误差，当网络输出与目标值存在差异时，这种误差会从输出层反向传播至隐藏层,最终根据误差信号调整各层之间的连接权值。

权值调整的数学表达式为：
Δw_ij = -η·(∂E/∂w_ij)

  • Δw_ij表示权值调整量
  • η为学习率(0<η≤1)
  • E为误差函数
  • ∂E/∂w_ij表示误差对权值的偏导数

权值调整的具体步骤

  1. 前向传播过程
    输入样本通过网络逐层传播，计算各神经元的输入和输出,直至得到网络的实际输出。

  2. 误差计算
    比较网络输出与期望输出,计算输出层各神经元的误差。

  3. 误差反向传播
    将输出误差反向传播至隐藏层,计算各隐藏层神经元的误差信号。

  4. 权值更新
    根据误差信号和学习率调整各层之间的连接权值：
    w_ij(t+1) = w_ij(t) + Δw_ij

  5. 迭代过程
    重复上述步骤,直到网络误差达到预设阈值或训练次数达到上限。

影响权值调整的关键因素

  1. 学习率选择

    bp神经网络 权值调整

    • 学习率过大可能导致震荡甚至发散
    • 学习率过小会显著降低收敛速度
    • 实践中常采用自适应学习率或学习率衰减策略

  2. 动量项引入
    加入动量项可以加速收敛并减少震荡：
    Δw_ij(t) = -η·(∂E/∂w_ij) + α·Δw_ij(t-1)
    为动量系数(0≤α<1)

  3. 权值初始化

    • 权值初始值应设置为较小的随机数
    • 避免对称初始化导致隐藏单元学习相同特征
    • 常见方法：Xavier初始化、He初始化等

  4. 正则化技术

    • L1/L2正则化防止过拟合
    • Dropout随机失活技术
    • 早停法(Early Stopping)

权值调整的优化策略

  1. 批量梯度下降与随机梯度下降

    • 批量梯度下降(BGD)：使用全部样本计算梯度
    • 随机梯度下降(SGD)：每次使用单个样本更新
    • 小批量梯度下降(MBGD)：折中方案，常用32-256的batch size

  2. 自适应优化算法

    • AdaGrad：适应性地调整各参数学习率
    • RMSProp：改进AdaGrad的累积梯度方式
    • Adam：结合动量与RMSProp的优点

  3. 二阶优化方法

    bp神经网络 权值调整

    • 共轭梯度法
    • 拟牛顿法
    • Levenberg-Marquardt算法(适用于中小规模网络)

实际应用中的注意事项

  1. 数据标准化
    输入数据应进行标准化处理(如Z-score标准化)，使各特征处于相近的数值范围,有利于权值调整的稳定性。

  2. 网络结构设计

    • 隐藏层神经元数量：太少会导致欠拟合，太多会导致过拟合
    • 隐藏层数：深层网络需要更复杂的权值调整策略
    • 激活函数选择：ReLU及其变体已成为主流选择

  3. 过拟合应对

    • 使用验证集监控模型性能
    • 实施正则化技术
    • 数据增强(对于特定类型数据)

  4. 训练监控

    • 记录训练集和验证集的损失曲线
    • 可视化权值分布变化
    • 监控梯度消失/爆炸问题

权值调整的数学推导(简化版)

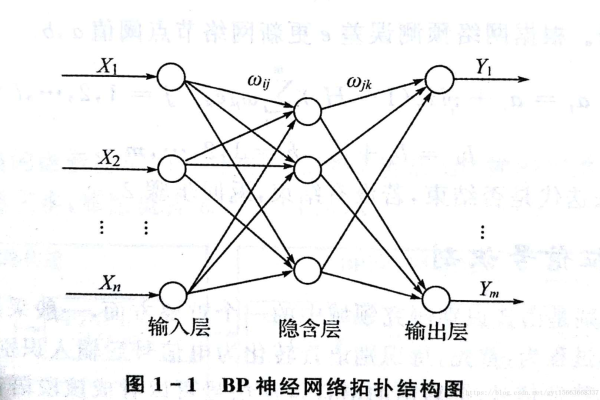
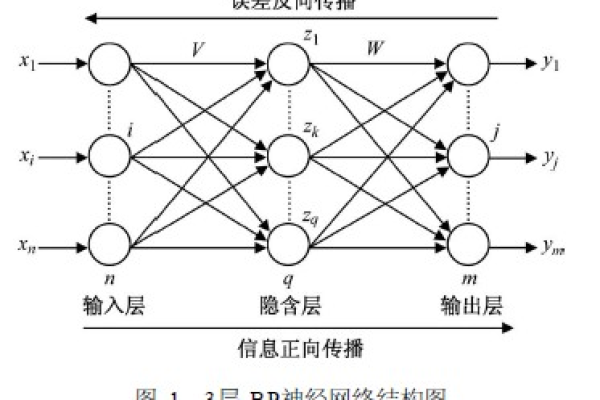
考虑一个三层BP网络(输入层-隐藏层-输出层),设：

  • 输入层到隐藏层的权值为w_ij
  • 隐藏层到输出层的权值为v_jk
  • 隐藏层使用sigmoid激活函数σ(z)=1/(1+e^{-z})

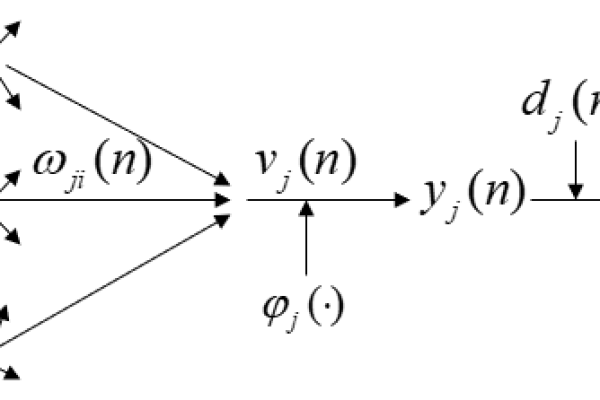
对于输出层神经元k，其误差信号为：
δ_k = (y_k – t_k)·σ'(z_k)

bp神经网络 权值调整

对于隐藏层神经元j，其误差信号为：
δ_j = σ'(z_j)·∑(δ_k·v_jk)

权值调整量为：
Δv_jk = -η·δ_k·h_j
Δw_ij = -η·δ_j·x_i

其中h_j为隐藏层神经元j的输出,x_i为输入层神经元i的输入。

BP神经网络的权值调整机制是其学习能力的核心所在，通过不断迭代的权值优化过程，神经网络能够逐渐逼近复杂的输入输出关系，理解权值调整的原理和影响因素，对于设计高效、稳定的神经网络模型至关重要，在实际应用中，需要根据具体问题和数据特点，灵活选择和组合各种优化策略,才能发挥BP神经网络的最大潜力。

参考文献与扩展阅读：

  1. Rumelhart, D. E., Hinton, G. E., & Williams, R. J. (1986). Learning representations by back-propagating errors. Nature, 323(6088), 533-536.
  2. Bishop, C. M. (2006). Pattern recognition and machine learning. Springer.
  3. Goodfellow, I., Bengio, Y., & Courville, A. (2016). Deep learning. MIT press.
  4. 神经网络与深度学习(邱锡鹏, 2020)
  5. 深度学习(花书)中文版(人民邮电出版社, 2017)

相关文章