从统计图分析数据的集中趋势
- 行业动态
- 2025-04-07
- 1
从统计图分析数据的集中趋势
在数据分析中,了解数据的集中趋势是至关重要的一步,它能够帮助我们快速把握数据的核心特征,为进一步的深入分析和决策提供基础,统计图作为一种直观的数据展示方式,在分析数据集中趋势方面发挥着重要作用,以下将详细介绍如何从不同类型的统计图中分析数据的集中趋势。
一、条形统计图
1、定义与特点
条形统计图是用一个单位长度表示一定的数量,根据数量的多少画成长短不同的直条,然后把这些直条按照一定的顺序排列起来,其特点是能够清晰地显示不同类别之间的数量差异,便于比较各类数据的相对大小。
2、分析集中趋势方法
观察条形高度:在条形统计图中,条形的高度(或长度)代表了对应类别的数量,通过比较各个条形的高度,可以直观地看出哪些类别的数据相对较多,哪些较少,较高的条形所对应的类别在数据中占比较大的份额,可能是数据的集中区域之一,在一个关于不同品牌手机市场占有率的条形统计图中,如果某品牌的条形明显高于其他品牌,那么该品牌的市场占有率较高,数据在一定程度上向该品牌集中。
计算频数分布:可以统计每个类别出现的频数,即每个条形所代表的数据个数,然后计算累计频数和频率,通过观察频率的分布情况来确定数据的集中趋势,若某个类别的频率较高,且其前后相邻类别的频率相对较低,那么该类别可能就是数据的集中区域。
| 品牌 | 市场占有率(%) |
| 品牌A | 30 |
| 品牌B | 25 |
| 品牌C | 20 |
| 品牌D | 15 |
| 品牌E | 10 |
从这个表格可以看出,品牌A的市场占有率最高,达到30%,说明数据在一定程度上向品牌A集中。
二、折线统计图
1、定义与特点
折线统计图是通过将数据点用直线连接起来而形成的图形,用于反映数据随时间或其他连续变量的变化趋势,它能够清晰地展示数据的增减变化情况,以及数据在不同阶段的发展态势。
2、分析集中趋势方法
观察数据波动范围:查看折线的波动幅度和范围,如果折线在某个区间内波动较小,且数据点相对密集,那么这个区间可能是数据的集中区域,在分析某公司月销售额的折线统计图中,如果发现某几个月的销售额数据点较为集中,且波动不大,那么这段时间的销售额可能处于相对稳定的集中状态。
寻找峰值和谷值:确定折线的最高点(峰值)和最低点(谷值),数据的集中趋势可能围绕这些极值点分布,如果存在多个峰值或谷值,需要进一步分析它们之间的关系和数据的分布情况,在一个产品销量的折线统计图中,某个时间段内的峰值可能表示该段时间内销量的集中爆发期,而谷值则可能代表销量的低谷期。
三、扇形统计图
1、定义与特点
扇形统计图(也称饼图)是用整个圆表示总数,用圆内各个扇形的大小表示各部分数量占总数的百分比,它可以直观地反映出各部分在总体中所占的比例关系,让人一目了然地看到数据的分布情况。
2、分析集中趋势方法
观察扇形面积大小:通过比较各个扇形的面积大小,可以确定各部分数据在总体中所占的比重,面积较大的扇形所对应的类别在数据中占比较大,是数据的主要集中部分,在一个关于学生兴趣爱好的扇形统计图中,阅读”兴趣所在的扇形面积最大,那么说明大部分学生对阅读感兴趣,数据在“阅读”这一类别上相对集中。
计算百分比:准确计算每个扇形所代表的百分比,并按照百分比的大小进行排序,通常情况下,累计百分比达到一定比例(如50% 80%)的部分可能是数据的集中区域,若前三个扇形的百分比之和达到60%,那么这三个类别可能是数据的主要集中方向。
四、直方图
1、定义与特点
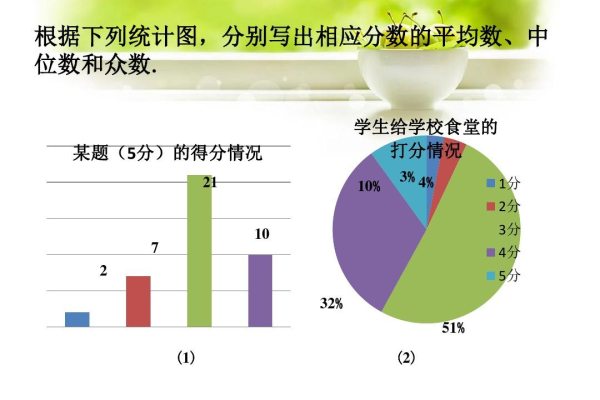
直方图是将数据分组后,用矩形的高度表示每组数据的频数或频率的一种统计图,它能够直观地展示数据的分布形态,如是否对称、是否存在偏态等,从而帮助我们分析数据的集中趋势和离散程度。
2、分析集中趋势方法
观察矩形高度:与条形统计图类似,直方图中矩形的高度代表了对应组别的频数或频率,通过比较各个矩形的高度,可以找出频数或频率较高的组别,这些组别的数据就是相对集中的数据,在一个学生成绩的直方图中,如果某个成绩区间对应的矩形最高,那么说明该成绩段的学生人数最多,成绩数据在这个区间内相对集中。
确定众数区间:众数是指一组数据中出现次数最多的数值,在直方图中,众数所在的组别通常是矩形最高的那个组别,通过观察直方图,可以大致确定众数所在的区间,从而了解数据的集中趋势,若某个成绩区间的矩形明显高于其他区间,那么该区间的中点值可近似看作众数,数据在该区间及其附近相对集中。
五、箱线图
1、定义与特点
箱线图是一种用于展示数据分布特征的统计图,它由箱体、上下须和异常值标记组成,箱体包含了数据的中间50%的数据,上下须分别延伸至数据的最小值和最大值(在一定范围内),异常值则用单独的点标记出来,箱线图能够直观地反映出数据的集中趋势、离散程度以及是否存在异常值。
2、分析集中趋势方法
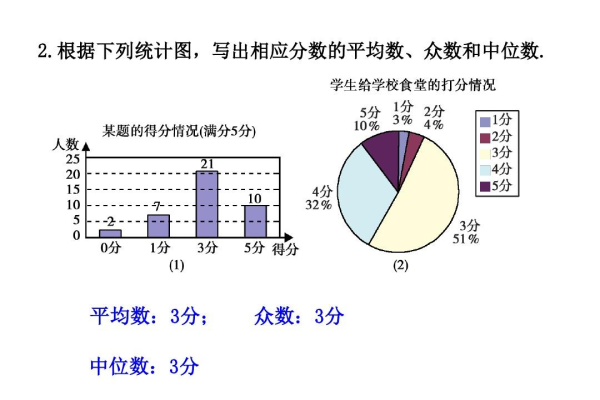
观察箱体位置:箱体的位置代表了数据的中间50%的分布范围,其中箱体中的中位数线(一般是一条横线)表示数据的中位数,中位数是将数据按照大小顺序排列后位于中间位置的数值,它是衡量数据集中趋势的一个重要指标,通过观察中位数线在箱体内的位置以及箱体的整体位置,可以判断数据的集中趋势,如果中位数线靠近箱体的上边缘,说明数据有向右偏态的趋势,但整体数据的集中区域仍在箱体范围内;如果箱体整体偏向某一侧,也反映了数据的集中趋势在相应方向。
分析四分位数间距:四分位数是将数据从小到大排序后,位于25%、50%(中位数)、75%位置的数值,四分位数间距(IQR)是上四分位数与下四分位数之差,它反映了数据中间50%的离散程度,较小的IQR值表示数据相对集中,较大的IQR值表示数据较为分散,结合箱线图的形状和四分位数间距,可以更全面地分析数据的集中趋势和离散程度,一个箱线图的箱体较窄且四分位数间距较小,说明数据相对集中在中位数附近。
FAQs:
1、如何从多种统计图中综合分析数据的集中趋势?
答:当有多种统计图时,首先要明确每种统计图的特点和适用场景,条形统计图适合比较不同类别的数据大小,折线统计图用于观察数据的变化趋势,扇形统计图展示各部分占比关系等,分别从每种统计图中提取关于数据集中趋势的信息,如条形图中的条形高度、折线图中的数据波动范围和极值点、扇形图中的扇形面积等,将这些信息进行综合对比和分析,找出数据的共性和差异,以确定数据的总体集中趋势,如果条形图中某类数据明显较高,同时在扇形图中该类数据占比也较大,那么可以更加确定该类数据是数据的集中区域之一。
2、在分析数据集中趋势时,如何避免受到异常值的影响?
答:在分析数据集中趋势时,要特别关注异常值的存在,对于异常值,可以根据具体情况进行处理,如果是由于数据录入错误等原因导致的明显错误值,可以直接剔除或修正,如果是真实的极端值,虽然不能随意剔除,但在分析集中趋势时可以适当考虑其影响,在使用平均数衡量数据集中趋势时,异常值可能会使平均数发生较大偏差,此时可以结合中位数等不受极端值影响的指标来综合分析,在绘制统计图时,也可以采用一些方法来减轻异常值的影响,如在箱线图中将异常值单独标记出来,以便更清晰地观察数据的分布情况和集中趋势。