bp神经网络 梯度

BP神经网络中的梯度

梯度在BP(反向传播)神经网络中扮演着核心角色，它决定了网络如何从错误中学习并逐步优化其权重参数,理解梯度及其计算过程是掌握神经网络训练机制的关键。

梯度的基本概念

在神经网络中，梯度指的是损失函数相对于网络参数的偏导数，对于网络中的每一个权重w，我们计算损失函数L对w的偏导数∂L/∂w,这个值告诉我们：

1. 损失函数在当前权重处的变化方向
2. 损失函数变化的速率
3. 权重应该调整的方向和幅度

梯度是一个向量，包含了损失函数对所有可训练参数的偏导数，在BP神经网络中,我们利用反向传播算法高效地计算这些梯度。

反向传播中的梯度计算

反向传播算法通过链式法则将误差从输出层逐层传播回输入层，计算各层参数的梯度,这个过程可以分为三个主要步骤：

1. 前向传播：输入数据通过网络，计算每一层的输出，直到得到最终输出
2. 误差计算：比较网络输出与真实值，计算损失函数
3. 反向传播：从输出层开始，反向计算梯度并更新权重

以一个简单的三层网络(输入层、隐藏层、输出层)为例,梯度计算过程如下：

对于输出层权重w⁽²⁾：
∂L/∂w⁽²⁾ = (ŷ – y) · σ'(z⁽²⁾) · a⁽¹⁾

对于隐藏层权重w⁽¹⁾：
∂L/∂w⁽¹⁾ = [∑(ŷ – y) · σ'(z⁽²⁾) · w⁽²⁾] · σ'(z⁽¹⁾) · x

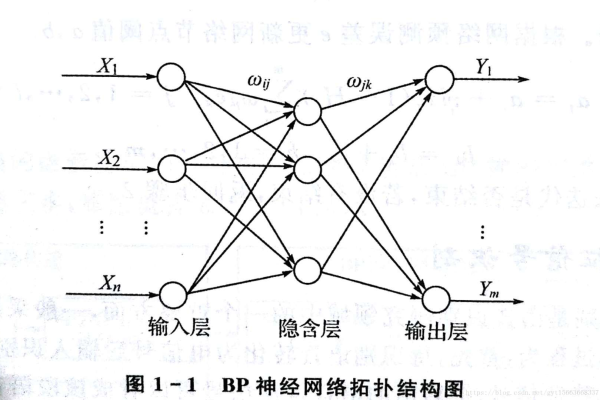
‘表示激活函数的导数，z表示加权输入,a表示激活输出。

梯度下降优化

得到梯度后,我们使用梯度下降法更新网络参数：

w = w – η·∇w

是学习率，控制每次更新的步长,梯度下降有多种变体：

1. 批量梯度下降：使用整个训练集计算梯度
2. 随机梯度下降(SGD)：每次使用单个样本计算梯度
3. 小批量梯度下降：折中方案，使用小批量样本计算梯度

现代神经网络通常使用带动量(Momentum)或自适应学习率(如Adam)的优化算法,这些都是在基本梯度下降基础上的改进。

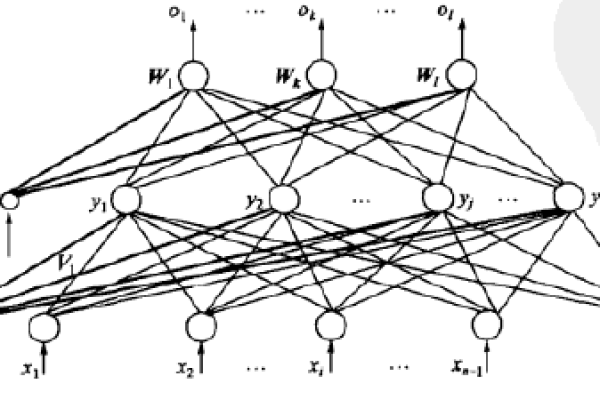
梯度消失与爆炸问题

在深层网络中，梯度可能随着反向传播而指数级减小(消失)或增大(爆炸),导致训练困难：

• 梯度消失：深层权重更新非常缓慢，网络难以学习
• 梯度爆炸：权重更新过大，导致数值不稳定

解决方案包括：

1. 使用ReLU等改进的激活函数
2. 合理的权重初始化(如He初始化)
3. 批归一化(Batch Normalization)
4. 残差连接(ResNet)

梯度检验

在实际实现中，梯度计算可能因编程错误而不准确,梯度检验是一种调试技术：

数值梯度 ≈ (L(w+ε) – L(w-ε)) / (2ε)

将数值梯度与解析梯度(反向传播计算)比较，确保两者接近，确认无误后应关闭梯度检验,因其计算成本高。

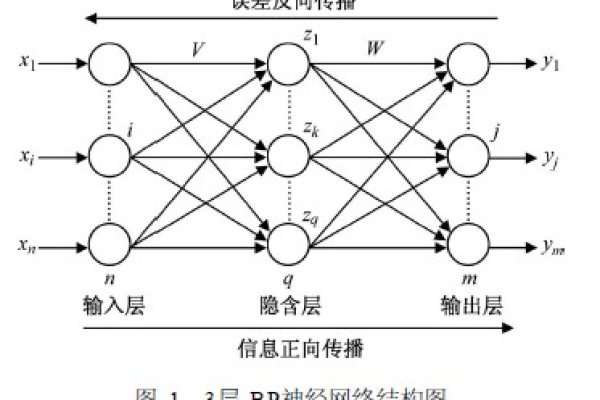
实际应用中的梯度处理

在实际训练中,我们还需要考虑：

1. 梯度裁剪：防止梯度爆炸，设置阈值限制梯度大小
2. 学习率衰减：随着训练进行逐渐减小学习率
3. 正则化：L1/L2正则化会修改梯度计算
4. Dropout：在训练时随机丢弃部分神经元，影响梯度流动

可视化理解

梯度可以直观理解为损失函数”地形”中的下坡方向,在参数空间中：

• 梯度方向指向最陡下降方向
• 梯度大小反映地形的陡峭程度
• 优化过程如同小球滚下山坡，寻找最低点

理解这一几何视角有助于调试网络训练问题。

梯度是BP神经网络学习的驱动力，反向传播算法提供了高效计算梯度的方法，掌握梯度相关概念和技术对于设计和训练神经网络至关重要，它直接影响模型的收敛速度、最终性能以及训练稳定性,现代深度学习中的许多创新都是围绕更有效地利用梯度信息而展开的。

引用说明参考了《Deep Learning》(Ian Goodfellow等)、CS231n课程笔记及多篇机器学习教育博客的核心概念,结合实践经验整理而成。