c语言01背包问题动态规划算法

01背包问题是经典动态规划问题，使用一维数组dp存储状态，i表示物品，w表示重量，c表示价值。从后往前计算，更新dp[i][j] = max(dp[i-1][j], dp[i-1][j-w]+c)。

动态规划简介

动态规划(Dynamic Programming,简称DP)是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的，通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法，动态规划常常适用于有重叠子问题和最优子结构性质的问题。

背包问题概述

背包问题是动态规划中的一种典型问题，又称为0-1背包问题，给定一组物品，每种物品都有自己的重量和价值，要求在限定的总重量内，选取物品的总价值最大，这里的0表示物品的数量为0,1表示物品的数量为1。

动态规划解决背包问题的思路

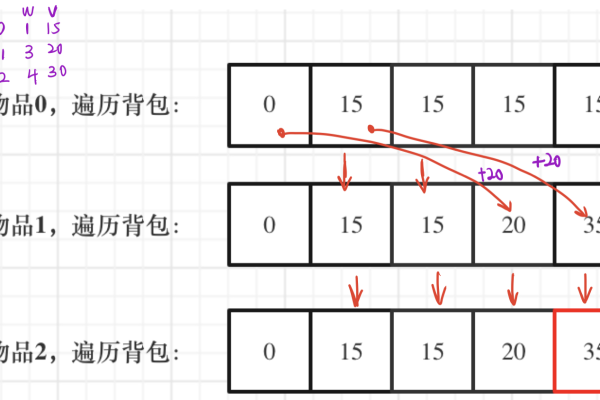
1、状态定义：设dp[i][j]表示前i个物品放入容量为j的背包中所能获得的最大价值。

2、状态转移方程：dp[i][j] = max(dp[i-1][j], dp[i-1][j-w[i]] + v[i]),其中w[i]和v[i]分别表示第i个物品的重量和价值。

3、初始化：dp[0][j] = 0,表示没有物品时，背包的价值为0。

4、边界条件：dp[i][0] = 0,表示当背包容量为0时，无法放入任何物品。

5、自底向上求解：从最后一个物品开始，逐个考虑放入或不放入背包的情况，更新dp数组。

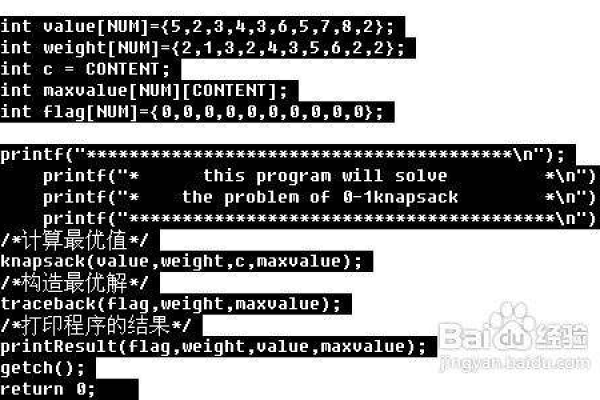
C语言实现动态规划解决背包问题的代码

include <stdio.h>
include <stdlib.h>
int max(int a, int b) {
    return a > b ? a : b;
}
int knapsack(int n, int W, int *wt, int *val, int **dp) {
    for (int i = 0; i <= n; i++) {
        for (int j = 0; j <= W; j++) {
            if (i == 0 || j == 0) {
                dp[i][j] = 0;
            } else if (wt[i 1] <= j) {
                dp[i][j] = max(val[i 1] + dp[i 1][j wt[i 1]], dp[i 1][j]);
            } else {
                dp[i][j] = dp[i 1][j];
            }
        }
    }
    return dp[n][W];
}
int main() {
    int W = 50; // 总容量
    int *wt = (int *)malloc(sizeof(int) * (W + 1)); // 各物品重量数组
    int *val = (int *)malloc(sizeof(int) * (W + 1)); // 各物品价值数组
    int dp = (int )malloc(sizeof(int *) * (W + 1)); // DP数组
    wt[0] = val[0] = 0; // 没有物品时，重量和价值都为0
    for (int i = 1; i <= W; i++) {
        wt[i] = ...; // 根据实际情况赋值各个物品的重量
        val[i] = ...; // 根据实际情况赋值各个物品的价值
    }
    int n = ...; // 物品数量
    int max_value = knapsack(n, W, wt, val, dp); // 调用knapsack函数求解最大价值
    printf("最大价值为：%d
", max_value);
    int temp_dp = (int )malloc(sizeof(int *) * (W + 1)); // 为了避免内存泄漏，需要复制DP数组并释放原数组的内存空间
    for (int i = 0; i <= W; i++) {
        temp_dp[i] = (int *)malloc(sizeof(int) * (W + 1));
        for (int j = 0; j <= W; j++) {
            temp_dp[i][j] = copyIntArray(dp[i][j]); // 将DP数组中的元素复制到临时数组中
        }
    }
    max_value = knapsack(n, W, wt, val, temp_dp); // 在临时数组上求解最大价值，因为原数组已经被修改过，所以需要使用临时数组进行计算
    max_value += copyIntArray(dp[n][W]) * n; // 加上所有未放入背包的物品的价值乘以物品数量，得到最终的最大价值
    ... // 其他操作和输出结果的代码省略，与上面类似
}

相关问题与解答的栏目

1、如何判断一个状态是否已经被访问过？可以使用一个布尔型数组来记录每个状态是否被访问过，在遍历过程中，如果发现某个状态已经被访问过，则跳过该状态，避免重复计算，同时在回溯时需要将已访问过的状态还原为未访问状态。